简介
轨迹相似度的计算有很多种方法,他们之间没有优劣之分,每种方法都有适合其发挥的使用场景。从思想上划分,轨迹的相似度计算大概可以分为三种:
- 结合路网信息的轨迹相似度计算
- 基于轨迹点匹配的计算方法
- 基于轨迹形状的计算方法
基于路网信息的轨迹相似度计算
这类计算方法都假设了知道路网信息的先验知识,并且轨迹点都很好的和路网信息相匹配。普适性较差,但适合特异性场景。
基于轨迹点匹配的相似度计算
最基础的基于轨迹点的轨迹度量方式,例如欧拉距离和曼哈顿距离等,其计算方式是轨迹之间的点一对一计算差异值,再累加起来。在轨迹长度不一致或者轨迹点采集频率不一致的情况下,都受到了限制。
为了解决在上述场景受限的问题,人们提出了轨迹扭曲距离的计算方式,直白点说就是两条轨迹相乘,组成一个矩阵,从矩阵的左上角到右下角找到一条路径,使其代价满足最大或最小,这个代价就用来描述轨迹的相似程度。这类思想的经典计算方法有DTW、LCSS、EDR、ERP等,他们之间的差异就是损失值的计算方式不一样。
- 上述4个方法,都可以对抗时间序列不统一的问题
- LCSS和EDR都是计算满足距离满足某个范围的相匹配的轨迹点对的数量。通过设置范围,算法具有一定的鲁棒性,但范围的选择对最终结果的影响也很大。
- ERP和DTW都是根据轨迹点之间的实际距离调节权重分配,将一条轨迹转变成(或者近似成)另一条轨迹。在这种语境下,这种思想要比LCSS和EDR要好。
- ERP是四种方式中唯一的Metric度量方式(这种方式的具体度量的特点,见备注部分),对于正则化的序列,具有很好的度量效果,但对于轨迹路径并不是很适合。
这四种度量方式最主要的贡献就是可以在序列长度不一致的情况下使用,并且可以对抗时间序列不一致的情况。但他们也有自己的局限:
- 相比较的两个序列需要比较平衡,不容易体现出序列的更多特征,例如加速减速等
- 受道路轨迹上的噪音影响,这些轨迹度量方式的效率受到很大限制
基于轨迹形状的相似度计算
这些轨迹的相似度计算方式是期望捕捉轨迹的形状特征,最为知名的算法就是Hausdorff距离和Frechet距离了。
Hausdorff
表述的是两个度量空间之间的距离,如下图所示,X,Y分别属于两个度量的空间。最简单的例子,就是两个度量空间都是点集,那么此时Hausdorff的思路就和基于轨迹点匹配的思路相似了。但是Hausdorff允许我们使用更复杂的度量空间,例如X是轨迹的点集,Y是轨迹的边集。需要注意的是Hausdorff为了达到最小,两个度量空间之间的元素匹配是任意的。
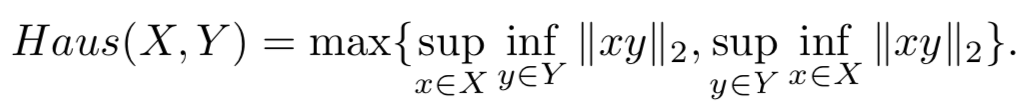
Frechet
Frechet最通俗的理解,就是人牵着狗散步,目标就是找到所需的最短的绳索长度。公式表示如下,需要找到两条轨迹之间最佳的对应规则,在这个规则下对应点(或者对应段)之间距离的最大值就是Frechet距离。因为需要找到最佳的匹配规则,所以Frechet算法的时间复杂度也比较高On^2log(n^2)。
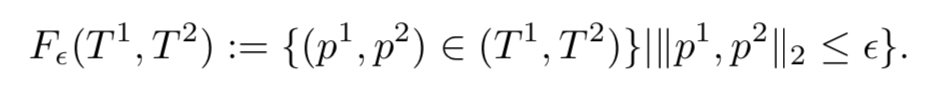
Discrete Frechet
因为Frechet距离的时间复杂度很高,因此提出了discrete Frechet距离,他简化了寻找最优匹配规则,使用了在轨迹扭曲距离里面的思想,生成轨迹矩阵W在W中计算discrete Frechet距离。
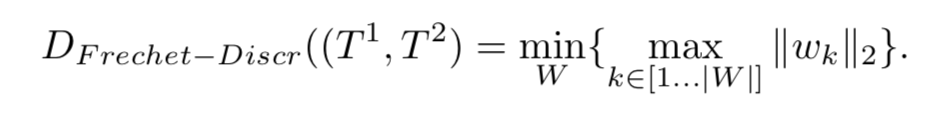
One Way Distance
OWD算法通过遍历一条轨迹中的轨迹点和另一条轨迹之间的距离的和的方式来进行计算。比较类似于求两条轨迹之间面积对应轨迹长度的平均值。算法思想如下图所示
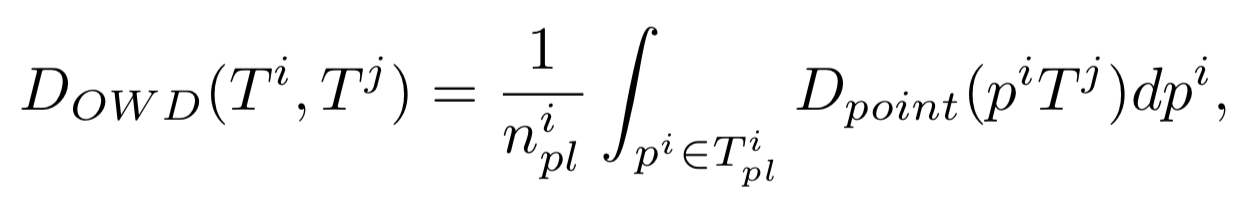
算法的一种具体实现方式如下图所示,其时间复杂度是n^2logn
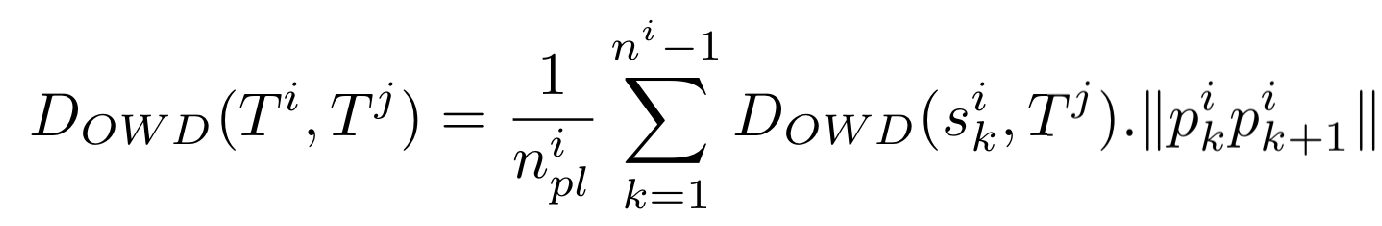
此外OWD算法也有一种基于网格的计算方式OWDg,时间复杂度会比上述的实现方式小很多。
总结
- Frechet和Discrete Frechet 距离都是满足metric类型的度量方式,满足三角不等式。他们在轨迹段之间的相似度度量是比较优异的,但是不适合做整体轨迹之间的相似度比较,(容易受到某个极端最大距离之间的干扰)。
- Discrete Frechet比Frechet距离的计算性能更优,但是它不是metric类型的度量。
- OWD算法可以将轨迹作为一个整体考虑进去,包括轨迹的形状和物理距离。算法的复杂度也比较高;OWD网格算法的时间复杂度低很多,但同时也受到了网格大小对最终结果的影响明显的问题。
SYMMETRIZED SEGMENT-PATH DISTANCE
SEGMENT-PATH DISTANCE 使用的度量方式的思想来源于OWD和Hausdorff。SPD的计算方式如下图。使用了平均值而不是Hausdorff的最大值,用于对抗噪声
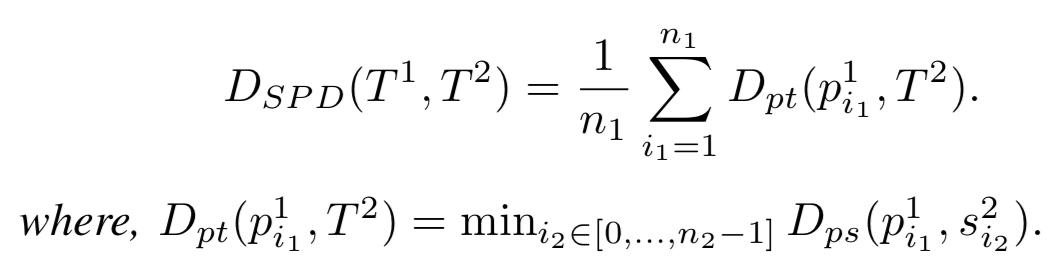
为了让SPD具备对称的特性,提出了SSPD,和SOWD的思想一样。

示例
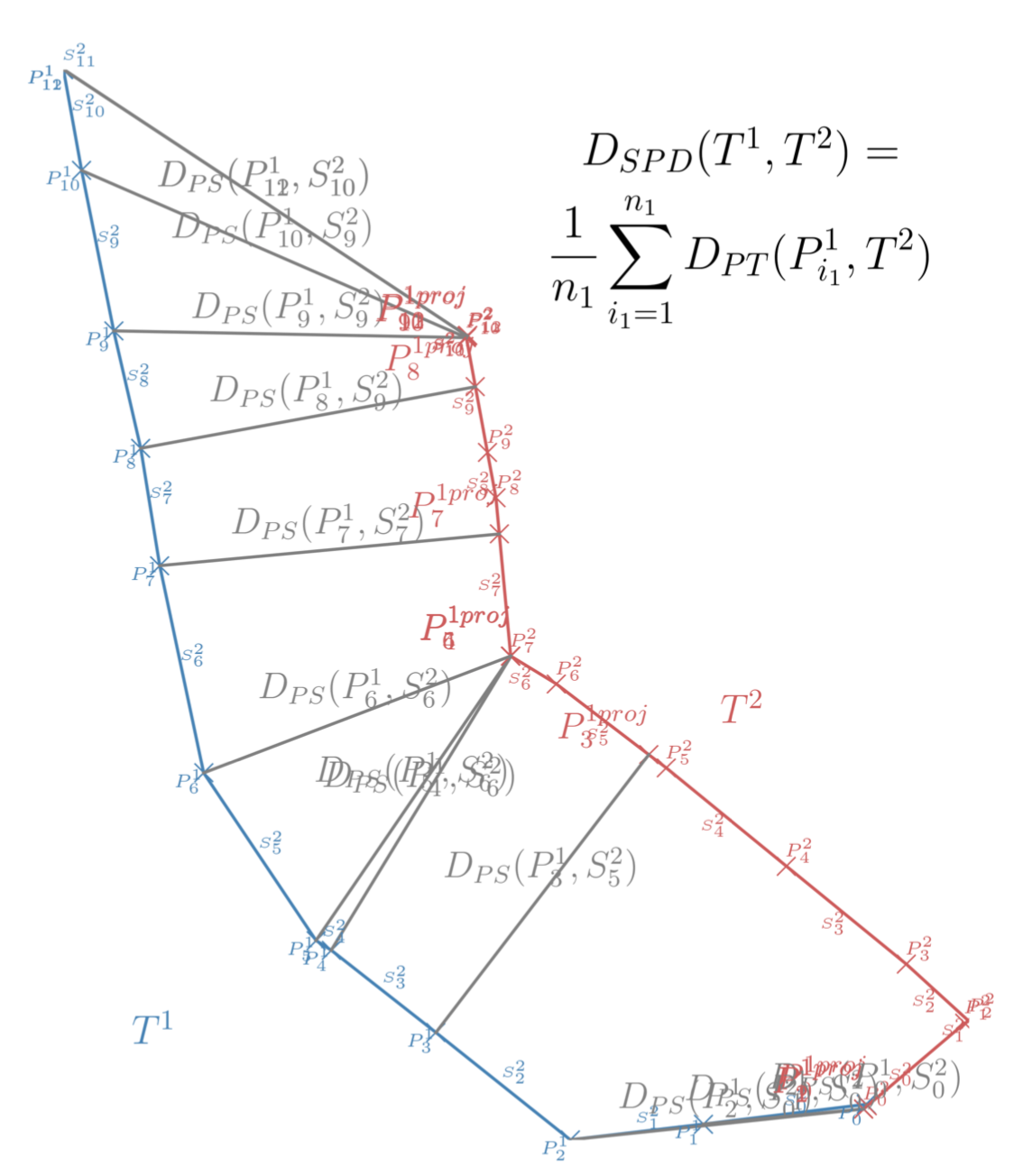
相比于OWD算法,作者认为SSPD:
- 更重视原有实际的数据信息。OWD使用了插值的思想对轨迹进行了补全(计算面积需要连续的轨迹)
- 没有手动设置参数的问题。OWD的网格大小等参数需要预先设置好
- 同时继承了OWD,在轨迹全局比较上的优势,不易受到局部轨迹对整体的相似性的影响(使用了均值而不是最值来表达相似性)
- SSPD在捕捉轨迹的形状和物理距离上的特性比较优秀,在最后的实验部分中有体现。
对轨迹进行聚类
聚类很容易想到的K-means算法因为需要度量方式遵守三角不等式,所以并不是适合在使用SSPD、LCSS或者DTW的时候使用。在文中作者提出了使用层次聚类和相似性传播,这两类聚类思想不需要相似度的计算遵循三角不等式。
聚类效果的评估
聚类效果的评估采用了类间距离和类内距离两个角度进行评估,在轨迹特定的场景下,论文给出了近似找出轨迹中心方式:找到一个类中到其他轨迹距离只和最小的那条轨迹。(感觉这个评估的对象是聚类的方法,并不是轨迹相似度的计算方式)
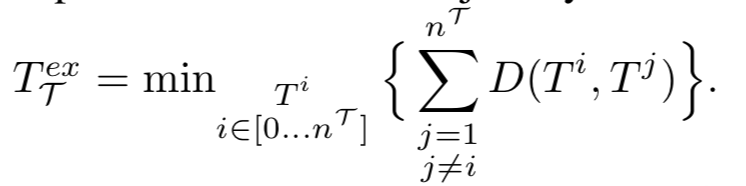
实验结果
除了使用single算法的层次聚类方式没有明显的效果之外,其他聚类方式都有明显的效果。同时类别达到一定数量之后,继续增加类别数量,也没有更明显的效果。
下图是SSPD距离,在使用不同类别的聚类方式时的效果图。
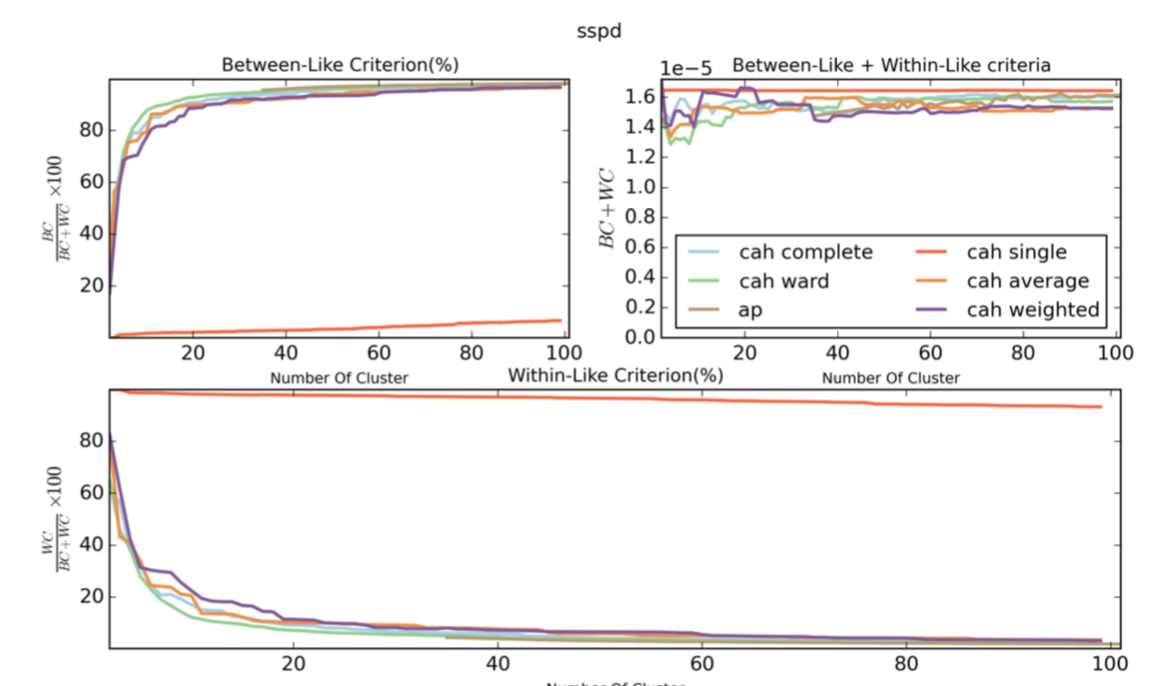
下图是在使用相同的聚类方式时,不同轨迹相似度计算方式的效果图
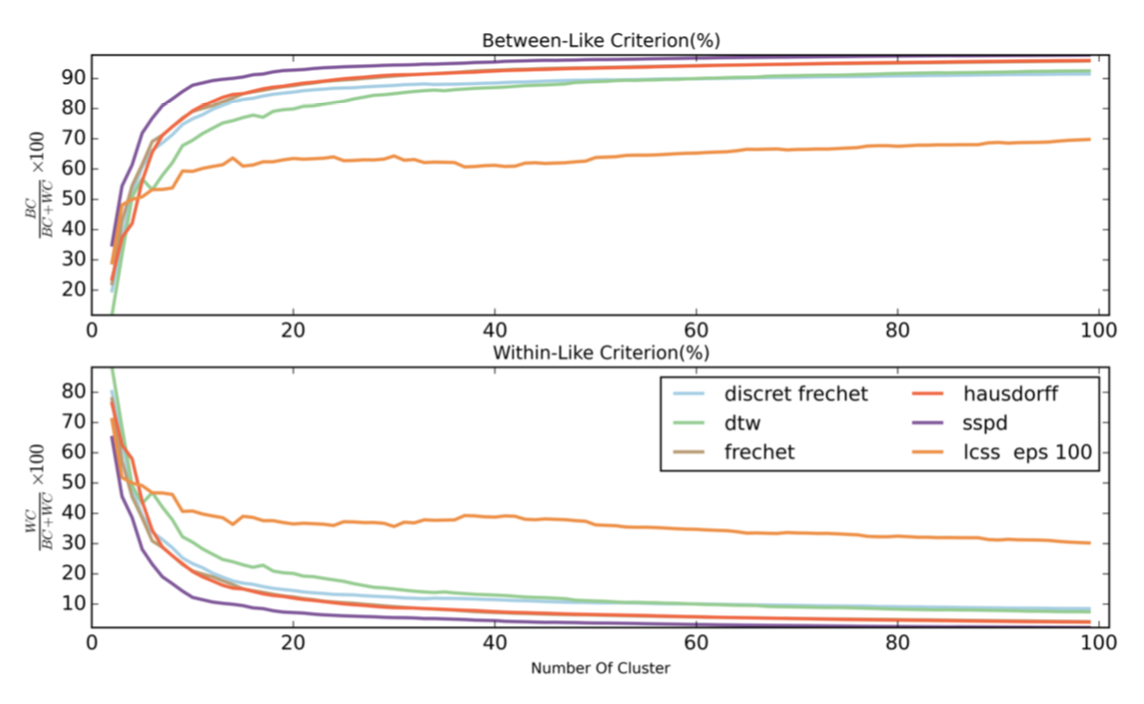
聚类的实际效果
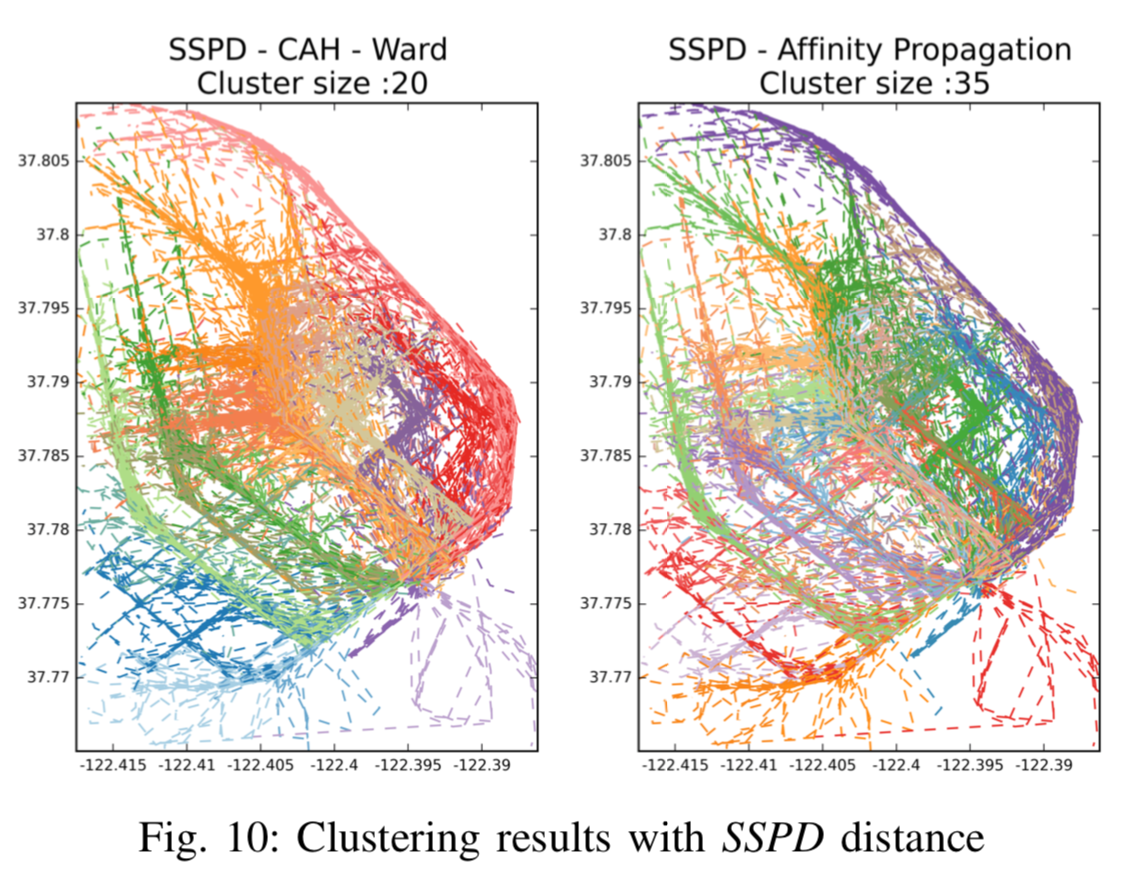
聚类形状上

附图
Notation
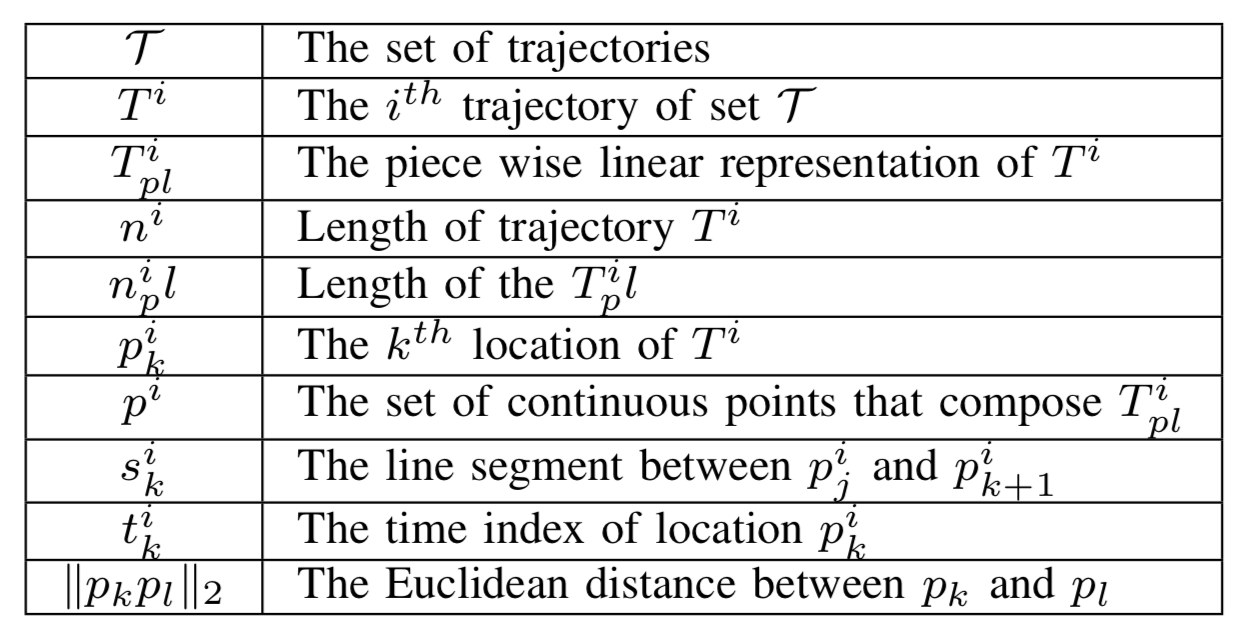
Re-Indexing based distance definition
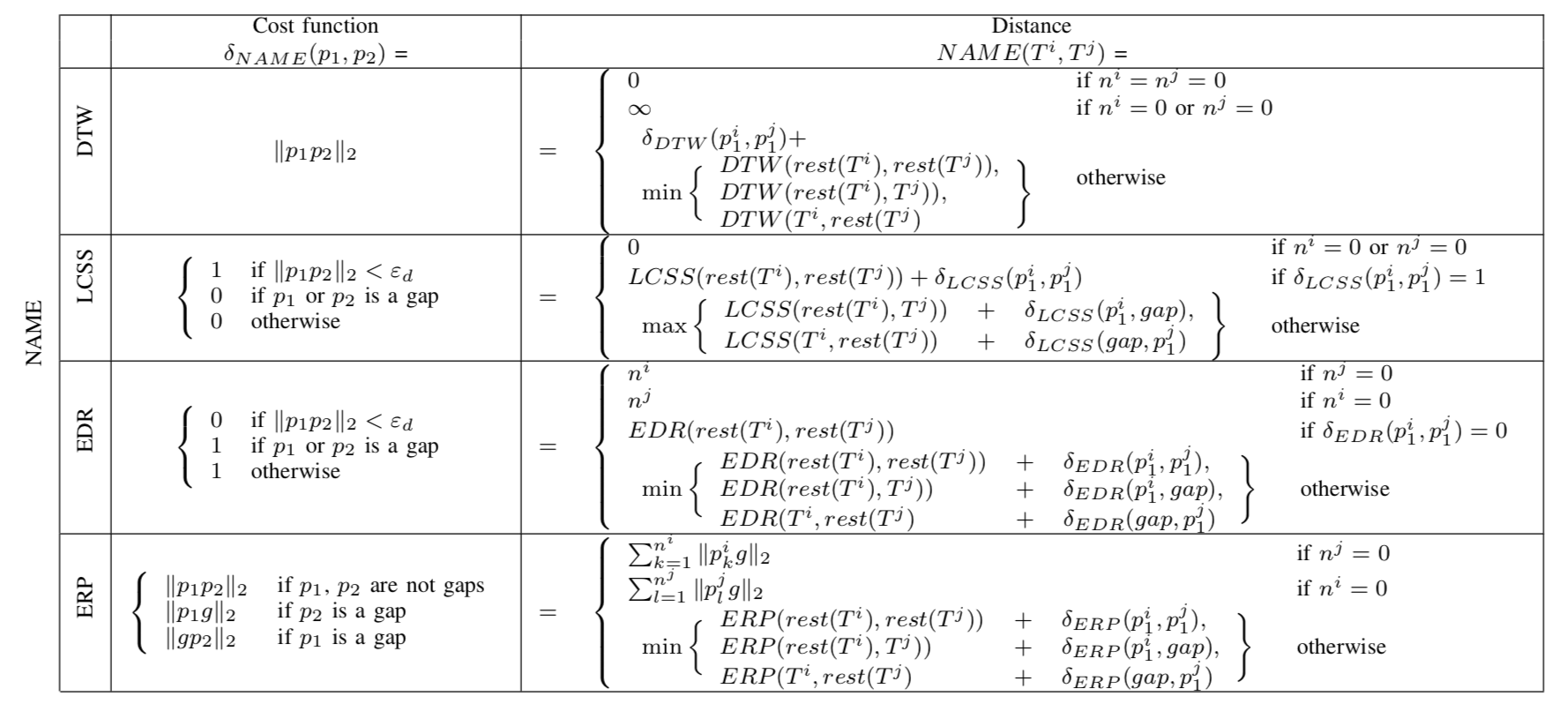
Metric Definition

Re-Indexing based distance properties
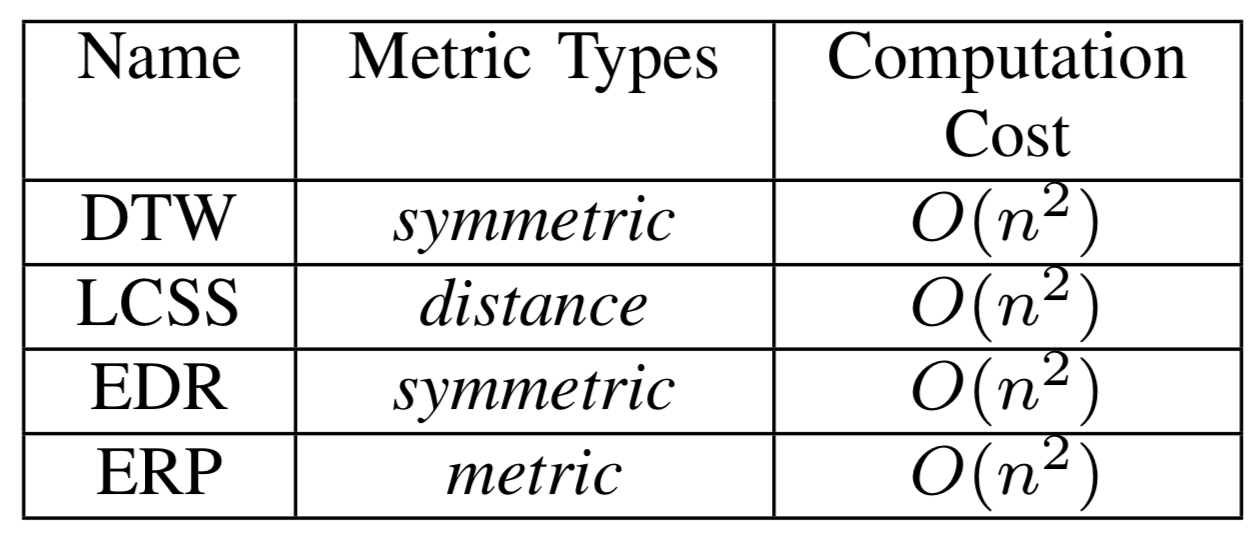
Shape based distance properties
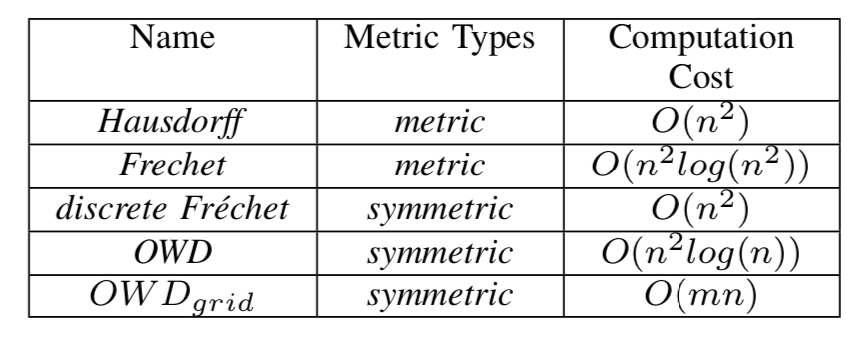
参考内容
《Review & Perspective for Distance Based Trajectory Clustering》