说明
本篇内容主要是包含了见过题目的收集,内容过多而且存在很多重复,不利于复习,只适合查询。内容的归纳可参考算法题目分类归纳(目录版)博客。
题目来源
题目来源为
关于标签
在归类策略中,会尽量根据题目最突出的特点进行归类,十分经典的多解法题目也会被重复放到不同的目录下。但其中一些稍微复杂的题目中,会有很多不同的基础部分来支持或者其他解法没有那么有特色的情况,对此将会采用标签的方式进行说明,可以通过搜索标签来发现一些基础组件在更复杂题目中的应用场景。下面是标签集合:
双端队列 动态规划 中心扩展 Manacher KMP BFS DFS 双向BFS 边界二分 双指针 单调栈 优先级队列 归并排序 滑动窗口 四边形不等式 数学归纳 约瑟夫问题 累加和 并查集 Kruskal Tarjan 前缀和 最接近目标 循环数组 最短路径 状态机
实现代码
参见 Github,最开始的很多题目缺少必要的注释和清晰的代码结构,再后续添加的过程中,正逐步改正该问题。
数据结构及其应用
栈
普通栈
232 用栈实现队列 剑指 Offer 09 用两个栈实现队列 面试题 03.04 化栈为队 CD6 由两个栈组成的队列 简单
保证每个元素最多只会进两次栈
单调栈
单调栈的逻辑切入点是:我遍历到当前列的时候,我能给栈中那些列赋予什么信息;去掉栈中这些列之后,栈中剩下的元素能给当前列什么信息。根据上述的逻辑判断在while循环中弹出元素时使用的大于小于号。
CD101 单调栈结构 简单 无重复元素,通过一次遍历获得结果
CD188 单调栈结构(进阶) 中等 有重复元素
-
对于每一个可能的位置
j(中间位置的元素),必定满足的两个条件:- 前面的最小值
pre_min_val小于当前值cur_val - 后面比
pre_min_val大的最小的元素pos_min_val小于cur_val
从后向前的每个元素左边的最小值,一定是非递减的,根据这个性质从后面向前遍历,维持一个栈,每次把小于
pre_min_val的元素踢出去,这样就获取了pos_min_val,若满足pos_min_val<cur_val,则该位置是合法位置。因为向前处理的过程中pre_min_val不断增大,所以栈中踢出的元素一定是之后不需要的元素。 - 前面的最小值
221 最大正方形 中等 CD16 求最大子矩阵的大小 中等 84 柱状图中最大的矩形的进阶版
1793 好子数组的最大分数 柱状图中最大的矩形的特例
1504 统计全 1 子矩形 困难 柱状图中最大的矩形的进阶版
316 去除重复字母 中等 CD121 删除多余的字符得到字典序最小的字符串 中等 使得返回结果的字典序最小
一个问题:栈中数据的大小顺序?
两个判断:什么时候可以压入栈中? 什么时候栈顶元素可以弹出?321 拼接最大数 困难 402题的进阶版本
CD102 可见的山峰对数量 中等 无重复值
503 下一个更大元素 II
循环数组
堆
优先级队列
215 数组中的第K个最大元素 中等 703 数据流中的第 K 大元素 简单 剑指 Offer 40 最小的k个数 简单 面试题 17.14 最小K个数 CD152 找到无序数组中最小的k个数 较难
自己实现一个堆排
480 滑动窗口中位数 剑指 Offer 41 数据流中的中位数的进阶版
延迟删除操作
集合
888 公平的糖果棒交换 快速判断数组中是否存在某个数字
1774 5690 最接近目标价格的甜点成本
最接近目标暴力穷举
队列
双端队列
- 239 滑动窗口最大值 剑指 Offer 59 - I 滑动窗口的最大值 简单 CD15 生成窗口最大值数组 简单
- 剑指 Offer 59 - II 队列的最大值 重复元素的情况
- 1438 绝对差不超过限制的最长连续子数组
滑动窗口
链表
单向链表
遍历链表
- 2 两数相加 面试题 02.05 链表求和 CD114 两个链表生成相加链表 入门
- 剑指 Offer 06 从尾到头打印链表 简单
- 面试题 02.02 返回倒数第 k 个节点 简单
- 61 旋转链表 倒数第k个节点的升级版
- 86 分隔链表 面试题 02.04 分割链表 中等
- 面试题 02.06 回文链表 简单 CD111 判断一个链表是否为回文结构 入门 CD112 判断一个链表是否为回文结构(进阶) 简单
- CD48 打印两个升序链表的公共部分 入门
反转链表
- 206 反转链表 剑指 Offer 24 反转链表 CD107 反转单向链表 入门 迭代 & 递归
- 92 反转链表 II CD108 反转部分单向链表 入门 反转m到n位置的部分
- 24 两两交换链表中的节点
- 25 K 个一组翻转链表 困难 CD119 将单链表的每K个节点之间逆序 简单 两两交换链表中的节点进阶版
删除链表节点
- 剑指 Offer 18 删除链表的节点 CD138 在链表中删除指定值的节点 入门 203 移除链表元素
- 19 删除链表的倒数第 N 个结点 剑指 Offer 22 链表中倒数第k个节点 CD49 在链表中删除倒数第K个节点 入门
- 83 删除排序链表中的重复元素 重复的元素,仅保留一个
- 82 删除排序链表中的重复元素 II 重复的元素,全部删除
- 面试题 02.01 移除重复节点
- 面试题 02.03 删除中间节点 CD157 一种怪异的节点删除方式 入门
- CD106 删除链表的中间节点 入门 正数第k个节点
- CD137 删除无序链表中值重复出现的节点 入门
重排链表
- 21 合并两个有序链表 剑指 Offer 25 合并两个排序的链表 CD159 合并两个有序的单链表 入门
- 23 合并K个升序链表
- 143 重排链表
- 5652 交换链表中的节点 可以按照交换节点的思想完成训练
- CD160 按照左右半区的方式重新组合单链表 入门
- CD113 将单向链表按某值划分为左边小,中间相等,右边大的形式 简单
- CD139 单链表的选择排序 入门
双向链表
相交链表
成环链表
快慢指针的形式,从head开始走,如果相遇了,说明有环路。设非环路长为\(l\),环路长度为\(q\),相遇位置是从环路起点之后又走了\(k\)。那么
fast指针的走的路长是:\(len_{fast}=l+a \cdot q+k\),
slow指针走的路长是:\(len_{slow}=l+b \cdot q+k\),
而且他们之间的关系是:\(len_{fast}=2 \cdot len_{slow}\),
处理之后\(2 \cdot l+2 \cdot b \cdot q+2 \cdot k=l+a \cdot q+k\),化简得,\(l=(a-2 \cdot b-1) \cdot q+(q-k)\),
此时让slow指针和头指针一起一个一个的走,直到相遇就是环形节点的头节点,因为他们第一次相遇的时候,满足上面的化简公式。
复杂链表
数组
数组操作
- 228 汇总区间 简单 返回恰好覆盖数组中所有数字的最小有序区间范围列表
- 剑指 Offer 21. 调整数组顺序使奇数位于偶数前面 简单
- 剑指 Offer 39. 数组中出现次数超过一半的数字
- 剑指 Offer 66 构建乘积数组 中等 CD35 不包含本位置值的累乘数组 入门
- 面试题 01.08 零矩阵
- CD24 奇数下标都是奇数或者偶数下标都是偶数 入门
- CD28 在数组中找到一个局部最小的位置 简单
- CD63 最大的leftMax与rightMax之差的绝对值 中等
- CD122 数组中两个字符串的最小距离 简单
矩阵操作
剑指 Offer 29 顺时针打印矩阵 54 螺旋矩阵 CD149 转圈打印矩阵 入门 59 螺旋矩阵 II
首先处理开头元素,然后根据规则打印按照次序每次循环依次拿掉矩形的上边,右边,下边和左边。每次拿掉之前都要判断矩形是存在的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14while(up<=down&&left<=right){
// 拿掉上边,上边界往下缩一下
for(i=up,j=left;j<=right;++j)ans.push_back(matrix[i][j]);
up++;
// 若矩形还存在,拿掉右边,右边界往左缩一下
if(left<=right&&up<=down) for(i=up, j=right;i<=down;++i)ans.push_back(matrix[i][j]);
right--;
// 若矩形还存在,拿掉下边,下边界往上缩一下
if(up<=down&&left<=right) for(i=down,j=right;j>=left;--j)ans.push_back(matrix[i][j]);
down--;
// 若矩形还存在,拿掉左边,左边界往右缩一下
if(up<=down&&left<=right) for(i=down,j=left;i>=up;--i)ans.push_back(matrix[i][j]);
left++;
}LCP 29 乐团站位 快速确定指定位置在顺时针打印时的序号
766 托普利茨矩阵 斜向遍历矩阵
子数组累加和
724 寻找数组的中心索引 简单
前缀和-
- 类似题目696 计数二进制子串 但技巧不一样
- 和1 两数之和 的技巧相似
-
倒排记录前缀和为k的最早位置,初始化压入mem[0]=-1;
525 连续数组 含有相同数量0,1的最长连续子数组
倒排记录0,1差值为k的最早位置;
-
倒排记录前缀和为k的位置数量,初始化压入mem[0]=1;
最优子矩阵
子矩阵问题从暴力求解开始思考,简化遍历步骤,优化算法。
5663 找出第 K 大的异或坐标值 225场周赛的题目,固定了子矩阵的左上角
面试题 17.23 最大黑方阵 中等 CD41 边界都是1的最大正方形大小 简单
通过预处理,快速判断可能的范围,压缩时间到\(O(n^3)\) 。
面试题 17.24 最大子矩阵 CD27 子矩阵的最大累加和问题 简单 剑指 Offer 42 连续子数组的最大和的进阶版本
221 最大正方形 中等 CD16 求最大子矩阵的大小 中等
单调栈上面两题都是通过简化遍历步骤来降低复杂度,即遍历子矩阵的边可能所在的行。
5655 重新排列后的最大子矩阵 CD16 求最大子矩阵的大小的进阶版本
-
利用有序表进行快速检索
头疼还未分类
CD51 分金条的最小花费 简单
霍夫曼编码1769 5686 移动所有球到每个盒子所需的最小操作数 困难
根据当前位置的情况,递推之后的位置
并查集
-
带权并查集,还没看懂
721 账户合并 中等 TODO
-
使用并查集处理同类项
5650 执行交换操作后的最小汉明距离 1202 交换字符串中的元素的进阶版
了解一下multiset的用法,可能会有帮助
-
leetcode的提示都没有让我想起这天是情人节
哈希
- 705 设计哈希集合 设计一个无重复数字的set
- 706 设计哈希映射
- 981 基于时间的键值存储
- 面试题 10.02 变位词组 中等
- 1726 同积元组 中等
- 1865 找出和为指定值的下标对
- CD62 设计有setAll功能的哈希表 入门
- 1743 5665 从相邻元素对还原数组
- 49 字母异位词分组
树
二叉树
二叉树的遍历
二叉树的遍历方式有先序遍历、中序遍历、后序遍历以及层次遍历。前三种方式都以通过递归的方式有效的实现,但是非递归的方式会显得复杂很多,这里简单记录一下非递归实现先中后序遍历的方式。(注释总结的感觉还是比较乱)
先序遍历
一个栈先压头节点,然后每次取中栈顶元素,按照打印其值,压入右孩子,再压入左孩子的方式进行实现
2
3
4
5
6
7
8
9
10
sta.push(head); // 压入头节点
// 对于每个节点的遍历顺序:父节点 --> 正序所有左孩子 --> 右孩子
// 压栈顺序正好反过来,(正序反过来就是压一个)
while(sta.size()){
node *t = sta.top(); sta.pop();
doSomething(t); // do something
if(t->right) sta.push(t->right);
if(t->left) sta.push(t->left);
}中序遍历
- 把头节点及其所有左孩子压入栈中;
- 取中栈顶元素cur, dosomthing; cur=cur.right;
- 重复步骤2,3。直到栈为空
2
3
4
5
6
7
8
9
10
11
node *cur=head;
// 遍历顺序
// 逆序所有的左孩子 --> 父节点 --> 右孩子的所有左孩子
// 压栈顺序正好反过来,(逆序反过来就是压所有)
while(cur||sta.size()){
while(cur){sta.push(cur); cur=cur->left;} // 压入cur及其全部的左孩子
cur=sta.top(); sta.pop(); // 取出栈顶元素
doSomething(cur); // do something
cur=cur->right;
}后序遍历
使用两个栈来实现,最终s2的弹出顺序就是后序遍历的结果
栈分别命名为
s1和s2;
- 将头节点压入s1
- 取中
s1的栈顶元素cur,然后依次压入其左、右孩子到s1中,然后将cur压入s2- 重复步骤2,直到
s1为空- 弹出
s2,就是遍历的结果
2
3
4
5
6
7
8
9
10
11
12
13
14
s1.push(head);
// 和下面用一个栈的思路反过来,后序遍历的反序,总是
// 父节点 --> 正序所有右孩子 --> 正序所有左孩子 压栈的时候反过来压(正序只压一个)
while(s1.size()){
node *cur=s1.top(); s1.pop();
if(cur->left) s1.push(cur->left);
if(cur->right) s1.push(cur->right);
s2.push(cur);
}
while(s2.size()){
node *cur=s2.top(); s2.pop();
doSomething(cur);
}使用一个栈来实现
一个栈sta,两个指针h,c;h指向最近一次弹出打印的节点,c指向栈顶的节点
- 先将头节点压入到栈中,初始化h为head,c为null
- 先令c等于栈顶元素,但不弹出
- c的左孩子不为null,且h和c的左右孩子都不相等:压入c的左孩子
- c的右孩子不为null,且h和c的右孩子不相等:压入c的右孩子
- 弹出并打印c,另h=c
- 重复步骤2,直到栈为空
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// h=head只是为了让h有个初始值,不和head的左右孩子以及空指针相等
sta.push(head); node *h=head, *c=nullptr;
while(sta.size()){
c=sta.top();
// 核心要义,左右孩子都打印完了,再打印父亲
// 打印父节点的之前,一定刚刚打印过了他的孩子(如果有的话)。注意这里的顺序
// 逆序所有左孩子 --> 逆序所有右孩子 --> 父节点 (针对所有节点都成立(若孩子不存在就顺位))
// 反过来是 父节点 --> 左孩子 --> 右孩子(注意这里一次只压入一个,和上面的都不同)
if(c->left&&c->left!=h&&c->right!=h) sta.push(c->left);
else if(c->right&&c->right!=h) sta.push(c->right);
else{
sta.pop();
doSomething(c);
h=c;
}
}
102 二叉树的层序遍历 103 二叉树的锯齿形层序遍历 剑指 Offer 32 - I 从上到下打印二叉树 剑指 Offer 32 - II. 从上到下打印二叉树 II 剑指 Offer 32 - III. 从上到下打印二叉树 III 面试题 04.03 特定深度节点链表 CD168 二叉树的按层打印与ZigZag打印 简单 层次遍历
- 队列的方式
- 两个栈的方式(阿里 Serverless 一面)
116. 填充每个节点的下一个右侧节点指针 简单 117. 填充每个节点的下一个右侧节点指针 II 中等 层次遍历的应用
124 二叉树中的最大路径和 后序遍历
199 二叉树的右视图 BFS && DFS
-
根据空位来判断,每遇到一个元素,占1多2,遇到终结符,占1
173 二叉搜索树迭代器 非递归中序遍历
938 二叉搜索树的范围和 非递归中序遍历
剑指 Offer 26 树的子结构 面试题 04.10 检查子树 判断一个棵树是不是另一棵树的子结构
剑指 Offer 34. 二叉树中和为某一值的路径 CD165 在二叉树中找到累加和为指定值的最长路径长度 简单 从某一节点向下,每次只能选择一个孩子
剑指 Offer 55 - II 平衡二叉树 面试题 04.04 检查平衡性 CD172 判断二叉树是否为平衡二叉树 入门 110 平衡二叉树 判断是不是平衡二叉树
面试题 04.12 求和路径 与剑指 Offer 26 树的子结构相同的结构
面试题 04.06 后继者 CD175 在二叉树中找到一个节点的后继节点 简单 中序遍历的后序节点
CD161 实现二叉树先序,中序和后序遍历 中等 递归 & 非递归
1600 皇位继承顺序 多叉树前序遍历
二叉树的重建
- 449 序列化和反序列化二叉搜索树 剑指 Offer 37 序列化二叉树 297 二叉树的序列化与反序列化 CD163 二叉树的序列化 入门 带有空节点的序列化和反序列化
- 剑指 Offer 07 重建二叉树 105 从前序与中序遍历序列构造二叉树 前序和中序重建二叉树
- 面试题 04.02 最小高度树 构造最小高度的二叉搜索树
- CD173 根据后序数组重建搜索二叉树 入门
- CD180 通过先序和中序数组生成后序数组 入门
二叉树的查找
236 二叉树的最近公共祖先 剑指 Offer 68 - II 二叉树的最近公共祖先 面试题 04.08 首个共同祖先 CD176 在二叉树中找到两个节点的最近公共祖先 入门 简化
- 若二叉树是一个搜索二叉树
- 若二叉树是一个有父指针 => 两个链表的第一个公共节点
- 若是一棵普通的二叉树
CD177 在二叉树中找到两个节点的最近公共祖先(进阶) 简单 CD178 在二叉树中找到两个节点的最近公共祖先(再进阶) 中等 多次查询
这都是啥??????
二叉搜索树
99 恢复二叉搜索树 困难 CD169 找到搜索二叉树中两个错误的节点 简单 找到二叉搜索树上被错误交换的两个节点
426. 将二叉搜索树转化为排序的双向链表 剑指 Offer 36 二叉搜索树与双向链表 897 递增顺序搜索树 CD156 将搜索二叉树转换成双向链表 简单
中序遍历CD167 找到二叉树中符合搜索二叉树条件的最大拓扑结构 中等
这都是啥??????
平衡二叉搜索树
- 1382 将二叉搜索树变平衡 将搜索树转换成平衡AVL搜索树
- 阿里面试题,给一个有序数组,将其转化成AVL搜索树
完全二叉树
- 222 完全二叉树的节点个数 完全二叉树的左右孩子至少有一个满二叉树,不是满二叉树的也是完全二叉树
- 1104 二叉树寻路
其他
- 1484 克隆含随机指针的二叉树
- CD162 打印二叉树的边界节点 中等 TODO
- CD170 判断t1树是否包含t2树全部的拓扑结构 入门
- CD171 判断t1树中是否有与t2树拓扑结构完全相同的子树 中等
- CD181 统计和生成所有不同的二叉树 简单
- CD182 统计和生成所有不同的二叉树(进阶) 中等
- CD187 派对的最大快乐值 简单
线段树
- 面试题 10.10 数字流的秩
- 327 区间和的个数 和为K的子数组的进阶,动态增加节点 & 将所有可能的情况映射成连续的整数
前缀树(字典树 Trie Tree)
336 回文对 从列表中找出所有字符串对,使得拼接之后满足回文结构
-
因为数据规模庞大,不能通过插入节点的方式构建出完整的树,需要通过规律计算出节点下面的孩子数量
因此在遍历上有点类似线段树 491 递增子序列 中等 所有递增子序列的最佳存储结构,前缀树
-
两种思路
- 先创建好树,然后在小于的限制条件下查找(通过位运算简化判断逻辑)
- 将需要的查询排序,每次查询之前,将满足小于条件的数字插入到前缀树中,可以省掉考虑小于的麻烦
-
对字符串的表示和压缩存储,加快索引速度
有序表
855 考场就座 最大平均通过率的进阶,考虑离开的情况
需要根据特定需要排序,并且动态添加和删除元素
-
利用有序表set快速检索大于等于某个值的第一个位置
字符串
基础操作
1807 5714 替换字符串中的括号内容 可当作替换空格的高级版
-
处理前缀0的方法
翻转
-
旋转数组与旋转字符串本质都是一样的,这里注意一题多解
- 使用额外空间进行求解
- 环形替换(最小公倍数与最小公约数)
- 三次翻转
编辑 & 匹配
这两类字符串题目的主要解题思想都是 递归 和动态规划
- 面试题 01.05 一次编辑
- 72 编辑距离 困难 CD43 最小编辑代价 中等
- 10 正则表达式匹配 剑指 Offer 19 正则表达式匹配 CD136 字符串匹配问题 中等
动态规划 - 44 通配符匹配 困难
括号
回文
回文类型的题目有四大类:
- 问题一:判断字符串是不是回文
- 问题二:找出最长回文子串
- 穷举子串,转化成问题一
- 动态规划,
dp[i][j]代表str[i:j]是否是回文子串- 中心扩展法,从每个中心出发,暴力计算
- Manacher,在中心扩展的基础上,利用存储的信息,加速判断
- 问题三:添加最少字符让字符串变成回文
- 动态规划,
dp[i][j]代表str[i:j]需要添加的字符- 在找到最长回文序列之后,剥洋葱
- 问题四:最长回文子序列
5 最长回文子串 中等
动态规划中心扩展ManacherSunday132 分割回文串 II
动态规划214 最短回文串 困难 通过在字符串前添加最少的字符,使得整体成为回文
Manacher-
Manacher算法的实现思想如下,根据历史上能扩展到最右范围的那个记录,来快速初始化当前的结果,例如
1
2
3
4
5
6
7
8
9
10
11
12
13
14// 为了统一处理,现将原来的字符串的首尾以及元素之间插入#
int i; // 当前遍历到的元素
int index=-1; // 能扩展到最右侧的记录的中心节点,初始化不存在,为-1
int pr=-1; // 能扩展到的最右侧的位置(开区间),初始化不存在,为-1
// ans[i] 记录的是从i位置出发的回文半径(包括自身)
// 对称过去的元素的回文长度不超过最右记录的那部分范围
// 若没有被包含到,则默认是1,即只包含自己一个元素的长度
ans[i] = pr>i ? min(ans[2*index-i], pr-i) : 1;
while(i+ans[i]<nums.size() && i-ans[i]>-1){
if(nums[i+ans[i]] == nums[i-ans[i]]) ans[i]++;
else break;
}
if(i+ans[i]>Pr) pr=i+ans[i], index=i;
// 最终i位置的元素的在原字符串的回文长度为 ans[i]-1; 1771 5688 由子序列构造的最长回文串的长度 516 最长回文子序列的进阶版
子串
28 实现 strStr() CD87 KMP算法 较难
KMPKMP算法的核心是构造next数组,next数组的作用,是快速判断B应该回退到那个位置开始比较
1
2
3
4
5
6
7// 从A中判断是否有子串B
if (A[i]!=B[j]){
j=next[j];
if(j==-1) ++i, ++j;
}else{
++i, ++j;
}next数组的计算方式如下
1
2
3
4
5
6next[0]=-1, next[1]=0;
for(i=2, cn=0;i<B.size;){ // i是当前要处理的字符,cn是前一个字符的next值
if(B[cn]==B[i-1]) next[i++]=++cn;
else if(cn>0) cn=next[cn];
else next[i++]=0;
}cn和i的关系如下图所示: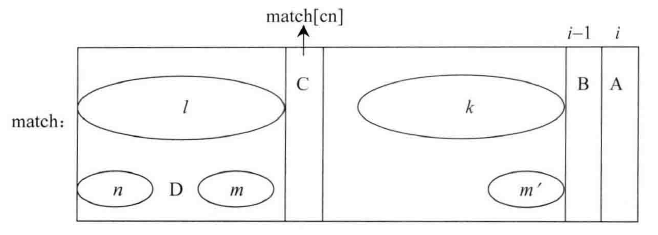
459 重复的子字符串 判断是否存在子串,通过不断重复得到原来的字符串
1764 5669 通过连接另一个数组的子数组得到一个数组 中等 可以通过快速子串匹配进一步加快速度
翻译
阿拉伯数字、英文表示、中文表示的翻译
阿拉伯数字转中文数字,参考解读。简单记录一下
- 将阿拉伯数字按万进行划分成节
- 节内划分为“”、“十”、“百”、“千”
- 节之间划分为“万”、“十万”、“百万”、“千万”、“亿”、“万亿”...
- 关于零的使用:
- 若小节之后都是0,则不加零,例如1,0000,中文为一万
- 小节之内的两个数字要加零,例如101,中文为一百零一
- 若千位是0,且前一小节无其他数字,则不用加零,否则加零,例如1,0100,中文为一万零一百;1,1000,中文为一万一千
其他
图
- 79 单词搜索
- 329 矩阵中的最长递增路径
- 399 除法求值
并查集 - 851 喧闹和富有
- LCP 07 传递信息
- 剑指 Offer 12 矩阵中的路径
- 剑指 Offer 13 机器人的运动范围
- 剑指 Offer 47 礼物的最大价值
- 面试题 08.02 迷路的机器人 中等 是否有必要回头?
- 面试题 04.01 节点间通路
- CD17 机器人达到指定位置方法数 简单
- 690 员工的重要性
转换路径
-
DFS -> BFS -> 双向BFS
CD123 字符串的转换路径问题 简单 面试题 17.22 单词转换的进阶版
BFS & DFS 同时使用的经典题目
无环图
- 684 冗余连接 中等
并查集
联通图
最小生成树
最小生成树有两种解法:逐个添加最优边的Kruskal和逐个添加最优顶点的Prim算法。
1584 连接所有点的最小费用 中等
Kruskal并查集1489 找到最小生成树里的关键边和伪关键边 困难
KruskalTarjan并查集一条边只能属于下列三种情况,其中有两种是比较好判断的
- 不在最小生成树中, 换言之, 先加入该边,无法组成最小生成树
- 在某个最小生成树中,但不在所有的最小生成树中
- 在所有的最小生成树中,换言之,少了它不能构成最小生成树
- 割点:删除该点之后,图分裂成两部分
- 桥(割边):删除该边之后,图分裂成两个部分
1579 保证图可完全遍历 困难
并查集证明先添加公共边是有效的
最短路径
最短路径有两种思路:
Dijkstra计算所有点到某个点的最短路径和距离,可以有环,权值需要为正,时间复杂度\(O(ElogV)\)Floyd计算所有点到所有点的最短路径和距离,不可以有环,权值可为负数
1631 最小体力消耗路径 中等
Dijkstra二分dfsbfs并查集Kruskal- 二分,判断可行性
- 构造最小生成树,dfs找出路径
- Dijkstra
778 水位上升的泳池中游泳 困难 与1631 最小体力消耗路径 中等一致的思路
Dijkstra二分dfsbfs并查集Kruskal
拓扑排序
-
排序算法,记录原顺序
拓扑排序是不一定有结果的,因此题目不一定有答案
三角形
-
- 审题:节点数量较少的时候,应该优先考虑使用矩阵来存储边
- 暴力枚举三角形的三重循环,起始位置递增
for(i=1;i<=n;++i) for(j=i+1;j<=n;++i) for(k=j+1;k<=n;++i) - 竞赛题目,十分遗憾,也暴露出了自己爱钻牛角尖,缺乏充分思考的致命弱点
- 新年之后第一场竞赛,祝福大家一切顺利!
算法思想及其应用
暴力
搜索
BFS
- 111 二叉树的最小深度 简单
BFSDFS - 752 打开转盘锁
BFS双向BFS - 815 公交路线
最短路径 - CD38 求最短通路值 中等
- 1765 5671 地图中的最高点 模拟水的蔓延
- 773 滑动谜题
- 909 蛇梯棋
DFS
-
树的遍历可以按照图来进行遍历,使用dfs遍历可以方便的管理当前节点的祖先情况,该题利用dfs遍历,记录祖先的情况,实现时间复杂度的降低
二分
基础二分
基础二分的应用
CD89 画匠问题 中等
动态规划四边形不等式注意left和right的初始化计算
852 山脉数组的峰顶索引 TODO 二分或者三分
边界二分
- 剑指 Offer 53 - I 在排序数组中查找数字 I 简单 有序数组中判断元素出现的次数
- 5643 将数组分成三个子数组的方案数 中等
累加和
有旋数组
154 寻找旋转排序数组中的最小值 II 剑指 Offer 11 旋转数组的最小数字 CD74 在有序旋转数组中找到最小值 简单 有重复
思路一:
- 判断整个范围是否有序,若有序直接返回最左侧的元素
- 左侧有序,查找右侧
- 左侧一定无序,查找左侧
- 无法判断是否有序,逐个遍历
思路二:
- 右侧一定无序,查找右侧
- 右侧一定有序,查找左侧
- 否则,--right;
33 搜索旋转排序数组 无重复,寻找给定值的下标
81 搜索旋转排序数组 II CD75 在有序旋转数组中找到一个数 简单 有重复,判断给定值是否存在
面试题 10.03 搜索旋转数组 中等 有重复,寻找某个值的位置且要求索引值最小
边界二分
其他
-
二分较长数组的下标,直接确定较短数组的分开条件 根据较短数组和较长数组之间是否满足左右两部分可以分开,确定,位置是否合理
57 插入区间 困难 二分只是一个小的实现组件
374 猜数字大小 简单 ??感觉和鸡蛋几楼碎很像,但不是。
尺取(双指针)
18 四数之和 N数之和问题
16 最接近的三数之和 三数之和的进阶版
42 接雨水 面试题 17.21 直方图的水量 纵向累加
双指针单调栈1791 5704 好子数组的最大分数 困难 求包含某个位置的子数组的最小值乘上子数组长度的最大值
单调栈的扩展应用最大矩形面积的变形题
滑动窗口
340 至多包含 K 个不同字符的最长子串 中等 159 至多包含两个不同字符的最长子串 进阶
992 K 个不同整数的子数组 困难 340 至多包含 K 个不同字符的最长子串 进阶
632 最小区间 困难 找到最小的区间,使得每个数组中至少有一个数字落入区间中
优先级队列归并排序好像和滑动窗口没啥关系
424 替换后的最长重复字符 中等 本人觉得思路并不是很容易理解
- 窗口维护的属性:窗口长度减去某个出现次数最多单词的出现次数\(<=k\)
- 在缩减左窗口的时候,不需要考虑出现最多的单词的次数变化,因为只有当新的出现次数最多的单词出现,窗口才有机会变的更大。
剑指 Offer 57 - II 和为s的连续正数序列,不定长滑动窗口
CD18 最大值减去最小值小于或等于num的子数组数量 中等 区间最值
双端队列1208 尽可能使字符串相等
前缀和二分查找找到最长的子串长度,可以在给定成本下修改成一样的-
定长滑动窗口,不断取消之前位置的影响,判断当前位置的翻转次数
状态机
-
状态转移如下图所示
排序
56 合并区间 合并重叠的区间
-
鹅厂要求快排的实现版本
315 计算右侧小于当前元素的个数 归并排序
327 区间和的个数 归并排序 & 在累加和数组头部添加一个0简化区间和的计算
912 排序数组 排序算法练习
剑指 Offer 51 数组中的逆序对 归并排序
倒排索引
- 3 无重复字符的最长子串 剑指 Offer 48 最长不含重复字符的子字符串 CD131 找到字符串的最长无重复字符子串 简单
动态规划滑动窗口 - 1371 每个元音包含偶数次的最长子字符串 状态压缩
- CD42 子数组异或和为0的最多划分 中等
递归 & 动态规划
动态规划类型的问题,在《程序员代码面试指南--刷题小结》中也有粗略的总结,但是缺少了整体思想的分析。根据《labuladong的算法小抄》中的解释,做点补充。
最开始的思路应该是,如何穷举所有的情况? 在能穷举出所有的情况的时候,找去其中存在的“重叠子问题”(需要找出其中存在的“状态”,争取尽量简单)来减少重复的计算量,同时需要保证具有“最优子结构”,即子问题间必须相互独立,最后确定状态转移方程。
递归
5 最长回文子串 中等 使用动态规划,并不是最优解
-
动态规划:p2, p3, p5 三个指针,分别指向乘以2,3,5之后获取到的最小的丑数,以此获取下一个丑数
set:取出最小的丑数,向其中加入其2,3,5之后的值
32 最长有效括号 困难 动态规划
377 组合总和 Ⅳ 动态规划
664 奇怪的打印机 动态规划
1269 停在原地的方案数 动态规划
62 不同路径 动态规划
740 删除并获得点数 动态规划,和打气球有点像
1473 粉刷房子 III 动态规划
斐波那契
- 509 斐波那契数 剑指 Offer 10- I 斐波那契数列
- 96 不同的二叉搜索树
- 1137 第 N 个泰波那契数
- CD183 斐波那契数列问题的递归和动态规划 较难
- CD184 斐波那契数列问题的递归和动态规划2 较难
- CD185 斐波那契数列问题的递归和动态规划3 较难
- CD129 0左边必有1的二进制字符串的数量 中等
动态规划 - 剑指 Offer 10- II 青蛙跳台阶问题 简单
- 面试题 08.01 三步问题
背包
背包问题根据labuladong的整理,可以分为0-1背包、子集背包和完全背包
416 分割等和子集
子集背包494 目标和
子集背包定义
dp[i]的含义是:子集和是i的拼凑方法数322 零钱兑换 CD12 换钱的最少货币数 简单
完全背包参考《程序员代码面试指南》中换钱的最少货币数,和我最开始的思考比较相近。
定义
dp[i]的含义是:拼凑出i的最少货币数思路的产生方式是:从特殊情况思考,0张和1张可以拼凑出的数值,再继续向后推广
1049 最后一块石头的重量 II
子集背包尽可能使数组划分成两部分之后的和相近,即使得去其中部分石头使得和尽可能的接近(仍要小于等于)总和的一半。
LCP 25 古董键盘 困难
分组背包-
类似:阿里笔试: m个项目,每个项目有收益和人力成本;n个人力,保证收益大于等于p的情况下,安排的方法数。
474 一和零 中等 多维背包
涂颜色
丢鸡蛋
非常经典的题目,有三种不同时间复杂度的解法
dp[k][n]\(k\)个鸡蛋\(n\)层楼,状态转移方程:1
2for i in range(1, n+1):
res=min(res, max(dp(k-1, i-1), dp(k, n-i))+1)base case:
1
2if k==1 return n
if N==0 return 0在上述方法中,因为
dp(k, n)若\(k\)是定值,\(n\)是变量,则函数是单调的,因此可以使用二分查找最佳i的位置重新定义状态
dp[k][m]\(k\)个鸡蛋,最多扔\(m\)次可以检查到的最高楼层,状态转移方程如下1
dp[k][m]=dp[k-1][m-1]+dp[k][m-1]+1 # 注意是相加的关系
base case:
1
2dp[0][:]=0
dp[:][0]=0
戳气球
经典动态规划问题,定义状态
dp[i][j]为打破\((i, j)\)气球,同时气球\(i\)和\(j\)还在时候的最大得分。在原来的气球序列的两侧添加上值为1的两个虚拟气球,dp[0][n+1]就是最终的答案,状态转移方程:
1 | for k in range(i+1, j): # 枚举最后打破的位置k |
石子游戏
两人博弈问题,本质上还是动态规划
给定数组,每次取左侧一个元素或者右侧一个元素,使用动态规划进行解决,首要问题是提取状态,在5687题目中,学习到了一种非常巧妙的状态表示方法,如下:
1 | dp[i][j] // 表示从数组前面取了i个数字,从后面取了j个数字。 |
1406 石子游戏 III 只从前面取
dp[i]从i位置开始先手可以拿到的最高分数
屠龙勇士
正确解法:反向思考从每个位置到终点需要最少的血量。正向思考难以权衡最少需要的血量和剩余的最大血量,会陷入局部最优。
可以尝试关联一下 CD53 加油站良好出发点问题,感觉有种微妙的联系
打家劫舍
买卖股票
买卖股票模型中最复杂的是带交易次数限制的。在动态规划中状态的定义是:dp[k][i][0/1] 表示在i天最多k次交易时持有或者不持有的最大收益;在状态转移方程中的体现是:第k次的持有状态不能由第k次未持有状态转移得到。
- 121 买卖股票的最佳时机 剑指 Offer 63 股票的最大利润
- 122 买卖股票的最佳时机 II
- 123 买卖股票的最佳时机 III 至多两次交易
- 188 买卖股票的最佳时机 IV 至多k次交易
- 309 最佳买卖股票时机含冷冻期
- 714 买卖股票的最佳时机含手续费
最长公共子序列
- 718 最长重复子数组
- 1035 不相交的线
- 1143 最长公共子序列 CD31 最长公共子序列 简单 CD33 最长公共子串 中等
- 115 不同的子序列 所有s的子序列中和t相等的数量
回溯
1723 5639 完成所有工作的最短时间
DFS剪枝最接近目标相似题目CD89 画匠问题,注意区别,画匠连续作画,但是这个任务分配不是连续的
TODO 给定时间判断此题是否可以满足要求,最接近目标的问题,暂时没有解题思路
1239 串联字符串的最大长度 TODO
数独
子集
全排列
有效括号
贪心
45 跳跃游戏 II 困难 CD92 跳跃游戏 入门 最少步数爬楼梯,给出每个台阶最多可以上跳数,求最少跳几次到最后一个位置
5691 通过最少操作次数使数组的和相等
二分查找为了填平差距,每次都找对差值影响最大的元素
也可以枚举sum值的方式,穷举所有的改变情况,需要使用二分查找来判断每次需要改变的次数
最长递增子序列
最长公共子序列问题也可以使用动态规划来解,但动态规划的时间复杂度是\(O(n^2)\),而贪心算法的时间复杂度是\(O(nlogn)\)。
354 俄罗斯套娃信封问题 CD29 信封嵌套问题 中等
排序贪心动态规划排序+最长递增子序列(贪心效率最高,动态规划也可以解)
排序原则是:更宽则更大、等宽更高小
排序之后的效果举例
2 3
5 4
6 7
6 4
现在针对第二列,只要第二列的值更大,则对应的宽也一定更大。此题转化成了单看第二列的最长递增自序列435 无重叠区间 中等 线段的连续递增序列
动态规划用起点去找,存的时候存终点
1691 堆叠长方体的最大高度 面试题 08.13的进阶版
1713 5644 得到子序列的最少操作次数 300 最长上升子序列的进阶版
看似最长公共子序列,但是因为有元素都不重复的限制,转化成了最长递增子序列,使用的算法思想也从动态规划变成了贪心,减少了时间复杂度。
加油站良好出发点
算是贪心的思想吗?
从一个盈余大于等于0的位置start出发,负债为0,走到最远位置end(没有剩余或者已走一圈),若走够了一圈,该起始点是一个良好出发点;否则该位置不是良好出发点。然后回退到上一个位置:
若盈余大于等于负债, 将(盈余-负债)送到end,负债改成0,继续向前走到最远位置,判断该点是否是良好出发点
否则,计算新的负债,因为有负债,所以该位置不是良好出发点
继续回退上一个位置,开始上述判断,直到所有点都检查一遍。
- 134 加油站 找到一个良好出发点
- CD53 加油站良好出发点问题 中等 找到所有良好出发点
分治
1755 5675 最接近目标值的子序列和 困难
最接近目标不能暴力穷据所有的,但是可以分两部分暴力穷举,然后再结合查找
395 至少有 K 个重复字符的最长子串 中等 1763 5668 最长的美好子字符串 简单
分治计算字符串中不满足要求的字符,根据这些字符对字符串进行切割,从子串中寻找最优答案
切割算法
1
2
3
4
5
6
7
8
9
10string s;
unordered_set<char> st;
int i, j, start, end; // 在[start, end)范围中,根据在st中的字符对字符串进行切分
i=start;
for(j=start;j<=end;++j){
if(j==end||st.count(s[j])){
func(s, i, j); // 找到一个切分段[i,j); 可能会出现i==j和i+1==j的无穷递归,需要在func最开始的位置进行拦截
i=j+1;
}
}滑动窗口
可以知晓最终答案中字符的类型数量是1-26中的一个值,通过穷举来获取答案。针对每次假设最终有k中类型字符,通过滑动窗口的思想去找每个位置能允许的最左位置
空间利用
数学问题相关
数字边界
- 7 整数反转 面试题 05.03 翻转数位
- 8 字符串转换整数 (atoi) 剑指 Offer 67 把字符串转换成整数 CD97 将整数字符串转成整数值 中等
- 29 两数相除
- 65 有效数字
状态机
计算
计算器
- 字符串处理类型的题目,先考虑好基本的处理模块,每个模块从哪一位开始处理,结束的时候在哪一位。
- 计算器类型的题目,只有加减的:先设置基数为0,默认加法,然后按照读数,读符号的循环开始处理
- 计算器类型的题目,加减乘除的:默认算术符号是'+',读数字,运算,更新符号
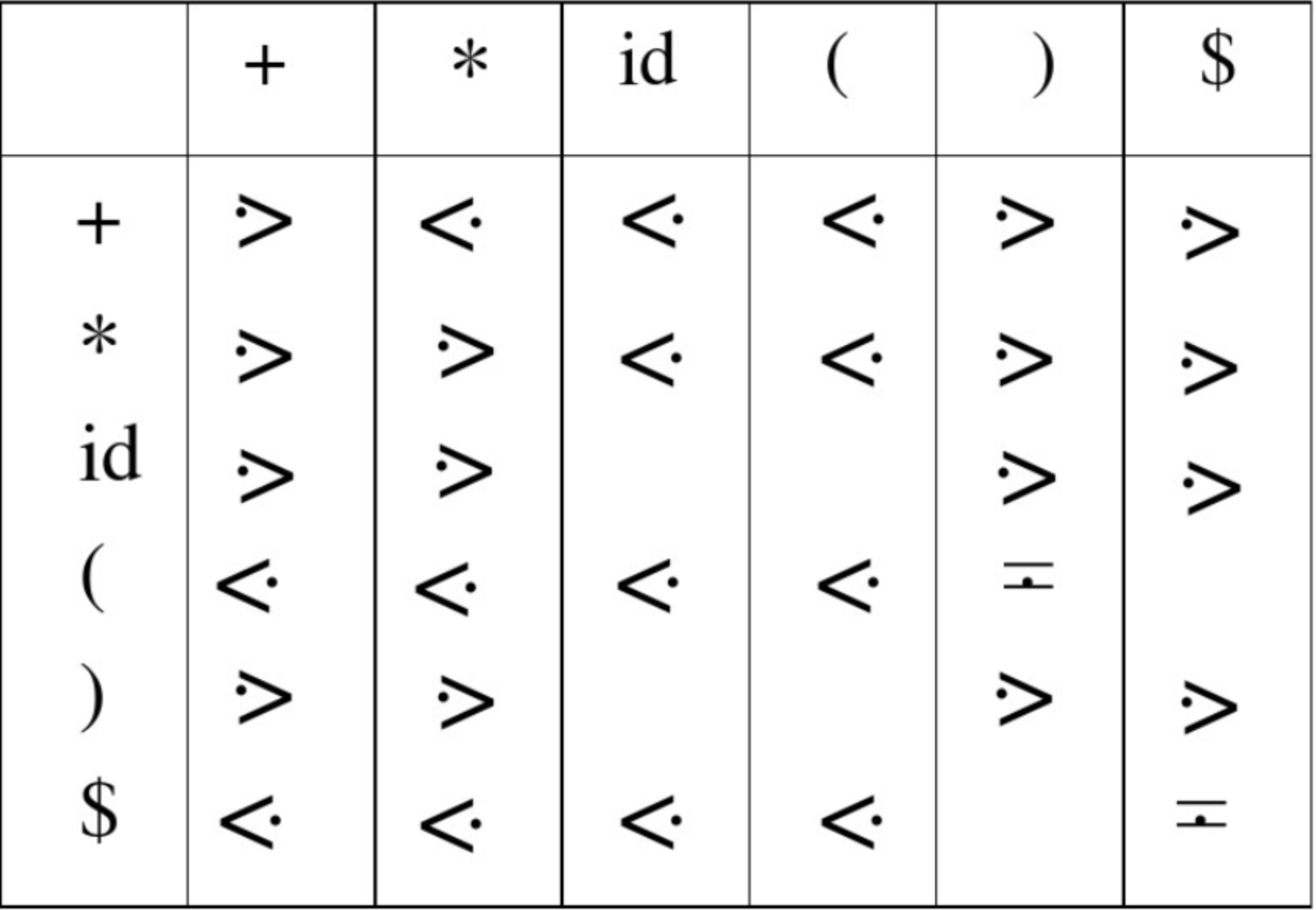
算术优先级表格法
定义如下的表达式的文法,是没有二义性的,开始符号为\[E\].(大写字母均是非终结符号) \[ \begin{array}{l} \mathrm{E} \rightarrow \mathrm{E}+\mathrm{T} \mid \mathrm{T} \\ \mathrm{T} \rightarrow \mathrm{T} * \mathrm{~F} \mid \mathrm{F} \\ \mathrm{F} \rightarrow(\mathrm{E}) \mid \mathrm{id} \end{array} \]
FirstVt的查找规则如下
- \(A\rightarrow a...\),将a加入A的Firstvt中
- \(A \rightarrow Ba...\),将a加入A的Firstvt中
- \(A\rightarrow B...\),将非终结符B的Firstvt加入A中
LastVt的查找规则如下,和FirstVt的规则正好相反
- \(A \rightarrow ...a\),将a加入A的LastVt中
- \(A \rightarrow ...aB\),将a加入A的LastVt中
- \(A \rightarrow ...B\),将非终结符B的LastVt加入A中
由此我们得出
FirstVt LastVt \(E\) \(\{(, id, *, +\}\) \(\{), id, *, +\}\) \(T\) \(\{(, id, *\}\) \(\{), id, *\}\) \(F\) \(\{(, id\}\) \(\{), id\}\) 按如下规则逐条扫描文法
\(E\rightarrow (E)\),则有\((=)\)
终结符在左边,非终结符在右边
- \(+T\),\(+ < FirstVt(T)\)
- \(*F\),\(*<FirstVt(F)\)
- ...
非终结符在左边,终结符在右边
- \(E+\),\(LastVt(E)>+\)
- ...
最终计算得到算术优先表格
一个更为详细的例子,参考
2
3
4
5
6
7
8
9
10
11
12
13
14
// + - * / ^ ! ( ) $ // 当前运算符
/* + */ '>','>','<','<','<','<','<','>','>',
/* - */ '>','>','<','<','<','<','<','>','>',
/* * */ '>','>','>','>','<','<','<','>','>',
/* / */ '>','>','>','>','<','<','<','>','>',
/* ^ */ '>','>','>','>','>','<','<','>','>',
/* ! */ '>','>','>','>','>','>',' ','>','>',
/* ( */ '<','<','<','<','<','<','<','=',' ',
/* ) */ ' ',' ',' ',' ',' ',' ',' ',' ',' ',
/* $ */ '<','<','<','<','<','<','<',' ','='
// 栈顶运算符
};
// 作者:dongzengjie用法,先在表达式左右两侧添加$号,形如
$1+2*(3+4)$,一个算数栈num,一个符号栈op。op初始化压如$,结束的时候再压如一个$。数字计算好之后直接入数字栈
符号:
- 若栈顶符号优先级低,继续压栈
- 若栈顶符号优先级相等,弹出栈顶,且不压栈
- 若栈顶符号的优先级更高,弹出符号进行计算(不需要循环处理,斜对角线的需要计算的优先级都是
>)
- 224 基本计算器 加减和括号
- 227 基本计算器 II 加减乘除
- 772 基本计算器 III CD128 公式字符串求值 中等 加减乘除和括号
- 150 逆波兰表达式求值
- 43 字符串相乘 中等
- 面试题 16.26 计算器
位运算
190 颠倒二进制位
分治分治分组交换的思想
-
异或运算是可逆的,不损失信息。这也是面试题 16.01 交换数字的基础
1825 5737 所有数对按位与结果的异或和 与、异或之间的计算方法
最大公约数
阶乘
CD57 有关阶乘的两个问题 中等 面试题 16.05 阶乘尾数的同类题,计算结果的二进制编码中最右边1出现的位置
上面两题都是计算某个因子的数量
快速幂
-
通过进制的方式
开平方
69 x 的平方根 微软面试题
牛顿法
进制转换
取余数
二进制
338 比特位计数
递推-
异或之后1的数量
X出现的次数
233 数字 1 的个数 困难 剑指 Offer 43 1~n 整数中 1 出现的次数 CD72 1到n中1的出现次数 较难
规律剑指 Offer 56 - II. 数组中数字出现的次数 II 137 只出现一次的数字 II 中等
利用状态转移记录出现的每个位置1出现的次数
几何
数学规律
分段乘积最大值
坐板凳
-
可以改变输入数组时:坐位置找重复座(n个数字n个可能性)
不可改变输入数组时:二分判断重复的元素出现在数组中的位置(书中此法针对的情况是n+1个数字对应了n个可能性,被坑了!)
面试题 17.19 消失的两个数字 坐位置找空位
448 找到所有数组中消失的数字 找出所有范围
1-n中没有出现的数字-
先动脑,考虑好所有情况再汇总分析,对我好难的一道简单题。
等概率
Rand
- 拒绝采样,rand7,通过两次调用,可以生成0-49个随机数,砍掉不满10个数的部分
- 在拒绝采样的部分,继续测试
- 进制来实现
蓄水池算法
从未知长度的数据流中随机取出k个数
思路是:每个数被最终选中的概率都是被选中的概率 * 不被替换的概率,伪代码如下。
1 | vector<int> calc(vector<int> arr, int k){ |
洗牌
逐次随机抽取
随机抽取一张牌,直到抽出所有的牌就是最终的洗牌结果
多次随机交换
随机抽两张牌进行交换,抽的次数足够多就完成了洗牌
Fisher–Yates shuffle算法
每次随机选取一个数,然后将该数与数组中最后(或最前)的元素相交换(如果随机选中的是最后/最前的元素,则相当于没有发生交换);然后缩小选取数组的范围,去掉最后的元素,即之前随机抽取出的数。重复上面的过程,直到剩余数组的大小为1,即只有一个元素时结束。
1
2
3
4
5
6
7
8
9void shuffle(int* array, int len) {
int i = len;
int j = 0;
while (--i>0) {
j = rand() % (i + 1);
swap(array[i], array[j]);
}
}
数学技巧
-
在接女朋友来深圳的时候,从核酸检测的问题,谈了起来,然后就毁了见面的好心情😅
1. 考虑每头猪的状态数量,主要是这个点没有想起来
2. x头猪组合成x方体,每头猪都能提供一个有毒的维度,最后确定有毒的桶
其他
模拟
简单
- 1002 查找常用字符
- 1207 独一无二的出现次数
- 1689 十-二进制数的最少数目
- 1688 比赛中的配对次数
- 349 两个数组的交集
- CD73 判断一个数是否是回文数 入门
- 455 分发饼干
- 485 最大连续1的个数
- 5641 卡车上的最大单元数
- 面试题 16.02 单词频率 中等
- 5653 可以形成最大正方形的矩形数目
- 283 移动零 可以趁机复习一下排序算法的稳定性
- 1128 等价多米诺骨牌对的数量
- 1742 5654 盒子中小球的最大数量
- 1752 5672 检查数组是否经排序和轮转得到
- 1758 5676 生成交替二进制字符串的最少操作数
- 566 重塑矩阵
- 561 数组拆分 I
- 485 最大连续 1 的个数
- 1768 5685 交替合并字符串
- 697 数组的度
- 867 转置矩阵
- 832 翻转图像
- 896 单调数列
- 1773 5689 统计匹配检索规则的物品数量
- 1785 构成特定和需要添加的最少元素
- 1784 检查二进制字符串字段
- 5701 仅执行一次字符串交换能否使两个字符串相等
- 5702 找出星型图的中心节点
- 1800 5709 最大升序子数组和
- 1603 设计停车系统
- 88 合并两个有序数组
- 781 森林中的兔子 中等
- 1817 查找用户活跃分钟数 中等
- 1816 截断句子
- 1006 笨阶乘 中等
- 1290 二进制链表转整数
- 1822 5726 数组元素积的符号
- 263 丑数
- 80 删除有序数组中的重复项 II
- 27 移除元素
- 26 删除有序数组中的重复项
- 1833 5735 雪糕的最大数量
贪心 - 1832 5734 判断句子是否为全字母句
- 66 加一
- 1486 数组异或操作
- 554 砖墙 中等
- 5838 检查字符串是否为数组前缀
- 1337 矩阵中战斗力最弱的 K 行
- 671 二叉树中第二小的节点
- 1893 检查是否区域内所有整数都被覆盖
- 1418 点菜展示表
- 面试题 05.06 整数转换
- 401 二进制手表 预计算
未分类 牛客
未做
- CD133 旋变字符串 较难
- CD68 正数数组的最小不可组成和 中等
- CD69 正数数组的最小不可组成和-进阶问题 简单
- CD47 表达式得到期望结果的组合种数 中等
- CD76 数字的英文表达和中文表达 中等
- CD67 路径数组变为统计数组 中等
- CD71 一种字符串和数字的对应关系 较难
- CD82 在两个排序数组中找到第k小的数 较难
- CD83 两个有序数组间相加和的Topk问题 简单
- CD90 邮局选址问题 中等
- 803 打砖块
数据库
待分类
-
梳理group by之后的聚合操作 & 理解join on语句中on的含义
多线程
锁 & 信号量
- 1114 按序打印
- 1115 交替打印FooBar
- 1116 打印零与奇偶数
- 1117 H2O 生成
- 1188 设计有限阻塞队列
- 1195 交替打印字符串
- 1226 哲学家进餐
- 1242 多线程网页爬虫
- 1279 红绿灯路口
Shell
题外篇
刷题历程
《程序员代码面试指南》是本好书,在牛客网上刷了80%的时候,我懒散了,丝毫没有做下去的动力,不过按照这本书的目录来刷题,的确会让人很愉快,因为你知道你自己做的题归属于哪一类。
为了增强自己的自信心,我开始在leetcode上刷《剑指offer》,然后就刷完了,记不清自己有什么收获,该错还是错,但是确实比第一遍做到时候要顺利很多。
某一天突然买了leetcode的会员,本着充分利用的会员的资源,我根据题号,筛选高频题刷起,刷着刷着就自闭了,题目之间的联系太少了,很多时候都变成为了AC而在做。(其实是因为困难和中等的占比太大了)
观察了身边的同学,我发现了《labuladong的算法小抄》,发现和《程序员代码面试指南》一样都是归纳整理之后的题目,不同点在于这本书的分类更偏向于框架思想,不看内容已经爱了,doing...
据说labuladong涉嫌抄袭,知乎链接, 尊重知识产权,如果真是抄袭的,不建议你再购买本书。
最近又看上了《程序员面试金典》,
10天不买零食小吃,就买下来...在此之前,重新归纳整理一遍做过的算法题吧,男人的嘴,骗人的鬼,书已经买了,零食一天都没少。眼看春招就要开始了,突然发现自己做题的能力貌似被遗忘了,有点难过。接下来以巩固复习为主!
5勋章、500道题、全站前5000,在2021年4月的最后一天,向5月问好~
在leetcode上已经有规律刷题半年的时间了,随着刚开始的时而癫狂、时而懒散,到慢慢地变成生活的习惯。感谢力扣伴我成长!
2021年7月31日,600题了。开始出现了松懈的苗头,这个月的补卡券都不够用的了。在这里也提醒自己要做题先想好思路,不要着急动手,少用debug,提升通过率。
2021年8月31日,700题了。回顾经典书籍中的算法题十分的重要而有意义。继续提醒自己,先想好思路再下手,注意边界问题的解决,提升通过率。
2021年9月20日,800题了。中秋节前夕,祝福团圆永远。
2021年11月10日 16:20,会员到期前的1分钟。想想去年今日,时间过的可真快。

致谢
- 感谢与我一起刷题的伙伴们,互相“嘲讽”,互相帮助,让我可以保持着刷题的动力, DML 401 加油!
- 感谢我的本科同学,ACM大佬,顶会论文作者,小帕,无数次帮我debug 乱麻般的代码,让我没有那么多烂尾,保持着继续下去的热情。
存储点:2021.08.08