WRY

Where Are You?
You are on the brave land,
To experience, to remember...

0%

算法题目分类归纳（目录版）

Posted on Edited on In
施工中。。。

说明

是对算法题目分类归纳（题库版）博客的整理归纳，主要目的是为了巩固算法题目的主要知识点，而不是包含全量的题目链接。

数据结构及其应用

栈

首先需要了解栈先进后出的特性，解决如下的问题

在基础栈问题的基础之上，增加一个栈中元素有序的问题，便衍生出了单调栈，这种特殊的数据结构，可以解决"求数组中每个位置往左或往右比当前元素大或者小的第一个位置"的问题，根据数组中有无重复元素，有难、易两种版本。

该类型题目的经典是

衍生类的题目还有

堆

堆分为最大堆和最小堆，涉及到堆排序，需要熟练掌握。

经典应用是优先级队列，基础的题目有

衍生类的题目还有：

堆排序

集合

集合也就是hash，特点就是在O(1)的时间内判断数字是否存在。利用这一特性，再结合一点小技巧可以有如下巧妙的题目：

队列

队列的特点是先进先出，基于该特点有简单类型的题目：

队列可以扩展到双向队列（deque），最大特点是，也可以从后面pop元素。该类型的题目：

链表

⚠️ 清理节点的next指针，避免next粘连。

链表类型的题目十分的灵活，基础的链表操作有如下类型的题目

在单向链表的基础之上，还有双向链表，经典题目有：

此外还有些复杂链表操作，如：

环形链表的入口节点

快慢指针的形式，从head开始走，如果相遇了，说明有环路。设非环路长为\(l\)，环路长度为\(q\)，相遇位置是从环路起点之后又走了\(k\)。那么
fast指针的走的路长是：\(len_{fast}=l+a \cdot q+k\)，
slow指针走的路长是：\(len_{slow}=l+b \cdot q+k\)，
而且他们之间的关系是：\(len_{fast}=2 \cdot len_{slow}\)，
处理之后\(2 \cdot l+2 \cdot b \cdot q+2 \cdot k=l+a \cdot q+k\)，化简得，\(l=(a-2 \cdot b-1) \cdot q+(q-k)\)，
此时让slow指针和头指针一起一个一个的走，直到相遇就是环形节点的头节点，因为他们第一次相遇的时候，满足上面的化简公式。

数组

数组能涉及到的题目数量十分的多，经典的题目有：

数组拓展一下便成了矩阵，相比于一维数组增加了一个维度，题目有：

利用数组下标和数组值之间的关系可以快速的实现一个并查集，基于并查集的题目有：

  • 判断连通分枝的数量

顺时针打印矩阵

只要矩阵存在就按顺序遍历上右下左的边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
while (up <= down && left <= right) {
  // 拿掉上边，上边界往下缩一下
  for (i = up, j = left;j <= right;++j) 
    ans.push_back(matrix[i][j]);
  ++up;
  // 若矩形还存在，拿掉右边，右边界往左缩一下
  if (left <= right && up <= down) 
    for (i = up, j = right;i <= down;++i)
      ans.push_back(matrix[i][j]);
  --right;
  // 若矩形还存在，拿掉下边，下边界往上缩一下
  if (up <= down && left <= right) 
    for (i = down, j = right;j >= left;--j)
      ans.push_back(matrix[i][j]);
  --down;
  // 若矩形还存在，拿掉左边，左边界往右缩一下
  if (up <= down && left <= right) 
    for (i = down, j = left;i >= up;--i)
      ans.push_back(matrix[i][j]);
  ++left;
}

树

树题目最多的就是二叉树，基本题目：

  • 树的前、中、后序遍历的递归和非递归实现版本以及层次遍历，参考
  • 基于二叉树遍历的二叉树重建、二叉树上的查找（最近公共祖先）

在二叉树上加一些特性就可以形成搜索二叉树，又回有些内容的题目

在二叉树上加上平衡的特性就形成了AVL树，涉及到AVL树的平衡调整

此外还有线段树、字典树（又称前缀树）、红黑树的应用（城市天际线）

先序遍历

非递归实现方式：

一个栈先压头节点，然后每次取中栈顶元素，按照打印其值，压入右孩子，再压入左孩子的方式进行实现

1
2
3
4
5
6
7
8
9
10
stack<node *> sta;
sta.push(head); // 压入头节点
// 对于每个节点的遍历顺序：父节点 --> 正序所有左孩子 --> 右孩子
// 压栈顺序正好反过来，（正序反过来就是压一个）
while(sta.size()){
  node *t = sta.top(); sta.pop();
  doSomething(t); // do something
  if(t->right) sta.push(t->right);
  if(t->left) sta.push(t->left);
}

中序遍历

  1. 把头节点及其所有左孩子压入栈中；
  2. 取中栈顶元素cur， dosomthing; cur=cur.right;
  3. 重复步骤2，3。直到栈为空
1
2
3
4
5
6
7
8
9
10
11
stack<node *> sta;
node *cur=head;
// 遍历顺序
// 逆序所有的左孩子 --> 父节点 --> 右孩子的所有左孩子
// 压栈顺序正好反过来，（逆序反过来就是压所有）
while(cur||sta.size()){
  while(cur){sta.push(cur); cur=cur->left;} // 压入cur及其全部的左孩子
  cur=sta.top(); sta.pop(); // 取出栈顶元素
  doSomething(cur); // do something
  cur=cur->right;
}

后序遍历

两个栈

使用两个栈来实现，类似先序遍历的反过来，最终s2的弹出顺序就是后序遍历的结果 栈分别命名为s1和s2

  1. 将头节点压入s1
  2. 取中s1的栈顶元素cur，然后依次压入其左、右孩子到s1中，然后将cur压入s2
  3. 重复步骤2，直到s1为空
  4. 弹出s2，就是遍历的结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
stack<node*> s1, s2;
s1.push(head);
// 和下面用一个栈的思路反过来，后序遍历的反序，总是
// 父节点 --> 正序所有右孩子 --> 正序所有左孩子 压栈的时候反过来压（正序只压一个）
while (s1.size()) {
  node* cur = s1.top(); s1.pop();
  if (cur->left) s1.push(cur->left);
  if (cur->right) s1.push(cur->right);
  s2.push(cur);
}
while (s2.size()) {
  node* cur = s2.top(); s2.pop();
  doSomething(cur);
}

一个栈

一个栈sta，两个指针h，c；h指向最近一次弹出打印的节点，c指向栈顶的节点

  1. 先将头节点压入到栈中，初始化h为head，c为null
  2. 先令c等于栈顶元素，但不弹出
  3. c的左孩子不为null，且h和c的左右孩子都不相等：压入c的左孩子
  4. c的右孩子不为null，且h和c的右孩子不相等：压入c的右孩子
  5. 弹出并 打 印c，另h=c
  6. 重复步骤2，直到栈为空
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
stack<node*> sta;
// h=head只是为了让h有个初始值，不和head的左右孩子以及空指针相等
sta.push(head); node* h = head, * c = nullptr;
while (sta.size()) {
  c = sta.top();
  // 核心要义，左右孩子都打印完了，再打印父亲
  // 打印父节点的之前，一定刚刚打印过了他的孩子（如果有的话）。注意这里的顺序
  // 逆序所有左孩子 --> 逆序所有右孩子 --> 父节点 （针对所有节点都成立（若孩子不存在就顺位））
  // 反过来是 父节点 --> 左孩子 --> 右孩子（注意这里一次只压入一个，和上面的都不同）
  if (c->left && c->left != h && c->right != h) sta.push(c->left);
  else if (c->right && c->right != h) sta.push(c->right);
  else {
    sta.pop();
    doSomething(c);
    h = c;
  }
}

字符串

字符串的题目都略有麻烦需要很耐心，有如下：

转化数值字符串

采用了状态机的解决思路，状态机如下图所示

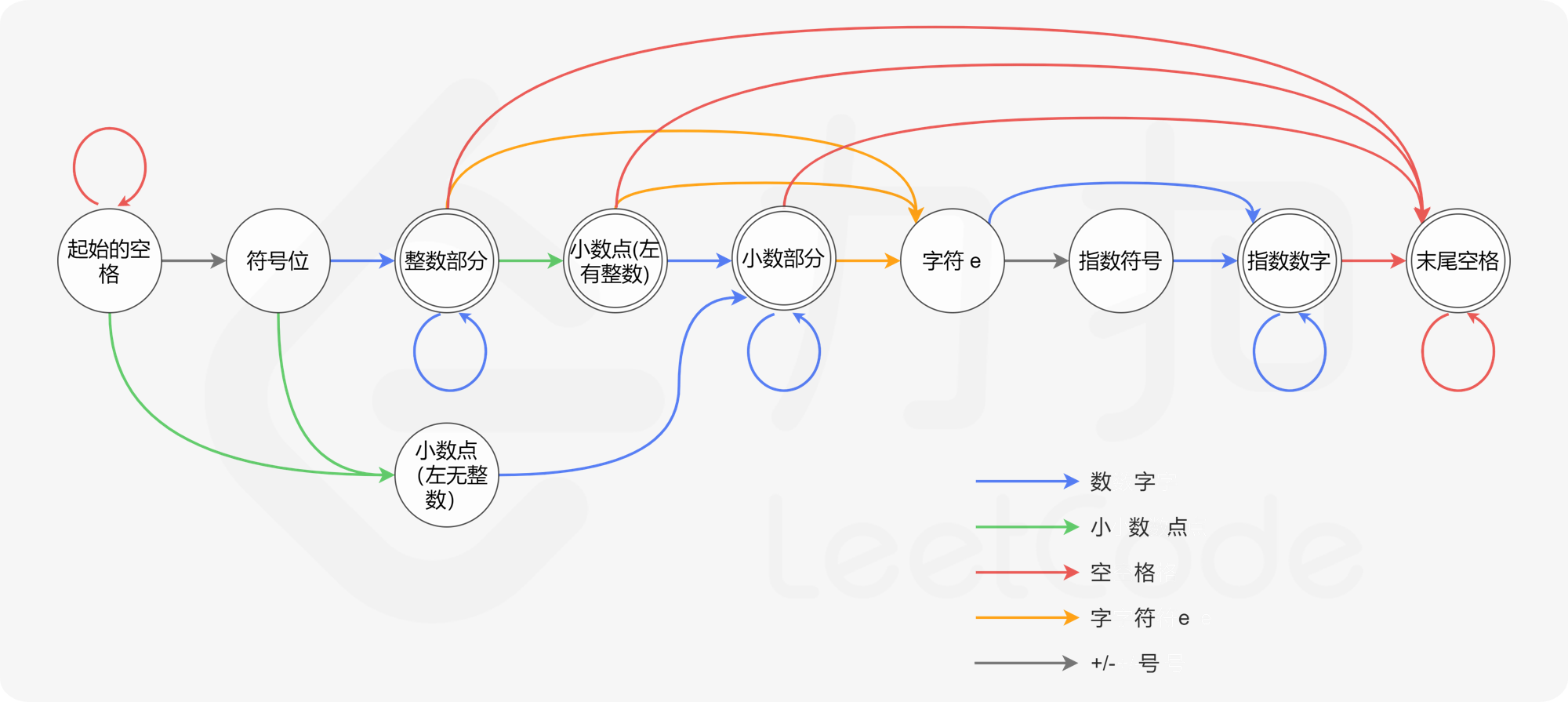
整数翻译成中文

  1. 将阿拉伯数字按万进行划分成节
  2. 节内划分为“”、“十”、“百”、“千”
  3. 节之间划分为“万”、“十万”、“百万”、“千万”、“亿”、“万亿”...
  4. 关于零的使用：
    1. 若小节之后都是0，则不加零，例如1,0000，中文为一万
    2. 小节之内的两个数字要加零，例如101，中文为一百零一
    3. 若千位是0，且前一小节无其他数字，则不用加零，否则加零，例如1,0100，中文为一万零一百；1,1000，中文为一万一千

Manacher算法

又称马拉车算法，参考《程序源代码面试指南》中的讲解，流程如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 为了统一处理，现将原来的字符串的首尾以及元素之间插入#
int i;  // 当前遍历到的元素
int index = -1;  // 能扩展到最右侧的记录的中心节点，初始化不存在，为-1
int pr = -1;  // 能扩展到的最右侧的位置（开区间），初始化不存在，为-1
// ans[i] 记录的是从i位置出发的回文半径（包括自身）
// 对称过去的元素的回文长度不超过最右记录的那部分范围
// 若没有被包含到，则默认是1，即只包含自己一个元素的长度
ans[i] = pr > i ? min(ans[2 * index - i], pr - i) : 1;
while (i + ans[i] < nums.size() && i - ans[i] > -1) {
  if (nums[i + ans[i]] == nums[i - ans[i]])
    ans[i]++;
  else
    break;
}
if (i + ans[i] > Pr) pr = i + ans[i], index = i;
// 最终i位置的元素的在原字符串的回文长度为 ans[i]-1;

KMP算法

参考《程序源代码面试指南》中的讲解

给定一个字符串str，判断其中是否存在match子串

辅助数组nextArr：nextArr[i]的含义是match[0:i-1]中，以match[i-1]结尾且不含match[0]的后缀子串与以match[0]开头的子串之间的最长匹配程度（其中的nextArr[i]为-1）。

有了nextArr数组之后的判断逻辑如下

1
2
3
4
5
6
7
// 从str中判断是否有子串match
if (str[i] != match[j]) {
  j = nextArr[j];
  if (j == -1) ++i, ++j;
} else {
  ++i, ++j;
}

nextArr数组的计算逻辑如下，注意初始状态

1
2
3
4
5
6
7
8
9
nextArr[0] = -1, nextArr[1] = 0;
for (i = 2, cn = 0; i < match.size;) {  // i是当前要处理的字符，cn是前一个字符的next值
  if (match[cn] == match[i - 1])
    next[i++] = ++cn;
  else if (cn > 0)
    cn = nextArr[cn];
  else
    next[i++] = 0;
}

cn和i的关系如下图所示：

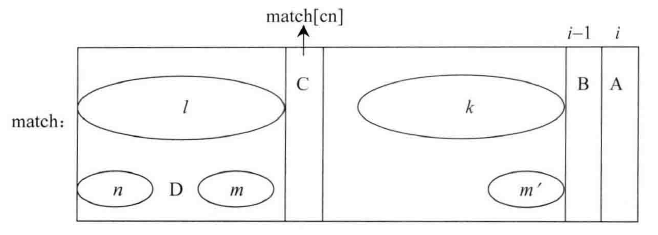
图

图的问题有如下几种：

最小生成树算法

最小生成树算法有Kruskal和Prim两种，

Kruskal会按照边的权重从小到大遍历，不产生环就可以保留边。

Prim会将顶点划分为两个集合，一个是树中的，另一个是不在树上的，每次会取不是树上的且离树上顶点最近的点添加上去。

他们的时间复杂度都可以认为是\(O(E*lgv)\)

最短路径算法

最短路径算法有Dijkstra和Floyd两种，

Dijkstra算法会将所有顶点分为S，D两个集合，初始化是只有S中有source node，同时记录D中顶点到S中的最短距离，每次都取最近的点v，将其加入S，并更新其最短路径。直到处理完所有的顶点。

Floyd会循环V次，每次都假设若顶点s和d之间的通过V时，更新s到d的最短距离。

他们之间的区别是

算法 解决目标 边 时间复杂度 空间复杂度
Dijkstra 单源最短路径 权重必须为正，可以有环 纯数组：\(O(V^2)\)
堆：\(O(E*lgV)\)		 \(O(V)\)
Floyd 多源最短路径 权重可有负，不可以有环 纯数组：\(O(V^3)\) \(O(V^2)\)

算法思想及其应用

暴力

优雅解法之前通常是暴力

BFS

DFS

二分

基础题目对我来说比较绕的是，旋转数组（有重复元素）中的最小值

唯一可以确定的是，若数组的一部分，最右侧的值比最左侧的大，那么这部分的元素一定是有序的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int findMin(vector<int>& nums) {
  int left = 0, n = nums.size(), right = n - 1, mid, k;
  while (left <= right) {
    if (nums[left] < nums[right]) return nums[left]; // [left, right] 有序
    mid = left + (right - left) / 2;
    if (nums[left] < nums[mid]) left = mid + 1; // [left, mid] 有序
    else if (nums[left] > nums[mid]) right = mid; // [left, mid] 存在旋转
    else { // 无法判断情况，顺序遍历
      for (k = left + 1;k <= right;++k) if (nums[k - 1] > nums[k]) break;
      return (k == right + 1) ? nums[left] : nums[k];
    }
  }
  return -1;
}

双指针

双指针的题目很多，就先把经典的题目列一下

接雨水

双指针确定左右的最矮边界，代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int trap(vector<int>& height) {
  int size = height.size();
  if (size < 2) return 0;
  // [left, right], lmax为[0,left)的最大值， rmax同理
  int left = 0, lmax = 0, right = size - 1, rmax = 0, ans = 0;
  while (left <= right) {
    // 保证了右边不漏（lmax<=height[right]），位置left的储水量由lmax决定
    if (height[left] < height[right]) {
      // 注意这里直接使用lmax就行，不能使用min(lmax, rmax)，因为右边届最高的高度还没有更新
      ans += max(0, lmax - height[left]);
      lmax = max(lmax, height[left++]);
    }
    else { // 保证了左边不漏（rmax<=height[left]），位置right的储水量由rmax决定
      ans += max(0, rmax - height[right]);
      rmax = max(rmax, height[right--]);
    }
  }
  return ans;
}

滑动窗口

状态机

排序

倒排索引

递归和动态规划

斐波那契

背包

背包问题是动态规划的经典问题之一，最基础的题目是

  • 一些物品每个都有一定的重量和价值，要在一个重为W的背包下能装到的最大价值的商品

在此基础之上，稍作变形，就能产生出一个套壳题目

上述两个题目的状态都是二维的，dp[i][w]考虑前i个物品时，在背包容量为w的情况下，能装下的最大价值，而且会存储所有w的情况。对比之下，有些题目的w种类数量庞大，不能全量储存，此种经典题目：

  • 盈利计划，m个项目，每个项目都有人力和成本，在给定人力限制下，保证收益大于等于p的情况下，可以安排的方法数。

此外还有一类经典钱币兑换问题：

在零钱兑换问题上有两种递推的改变：

类似的题目可参考古董键盘。

零钱兑换

零钱兑换需要使用的最少钱币数量，题目

从暴力解法开始，使用前\(i\)张纸币，拼出\(t\)数量的钱币的最少钱币数量。找到一种状态dp[i][t]

逐渐优化该问题，我们可以不关心使用了哪些纸币，只关系在t的目标下，需要使用的最少货币数量，转移方程如下

1
2
3
4
5
6
7
8
9
10
11
vector<int> dp(amount + 1, -1);  // 以amount为状态
dp[0] = 0;
for (i = 1; i <= amount; ++i) {
    x = INT_MAX;
    for (j = 0; j < n; ++j) {
      k = i - coins[j];
      if (k >= 0 && dp[k] != -1) 
        x = min(x, dp[k]);
      if (x != INT_MAX) dp[i] = x + 1;
    }
}

零钱兑换的组合数，题目

零钱兑换的方案数量，最优的解法也是以拼出t数额作为状态，状态转移方程如下

1
2
3
4
5
6
7
vector<int> dp(amount + 1);
dp[0] = 1;
for (auto& p : coins) { // 每多一种硬币对结果的影响
    for (int i = p; i <= amount; i++) {
      dp[i] += dp[i - p];
    }
}

零钱兑换的排列数，题目

零钱兑换的组合数的做法，和零钱兑换的方案数十分的类似。以拼出t数额为状态，状态转移方程如下：

1
2
3
4
5
6
7
8
9
10
11
12
int dp[target + 1];
dp[0] = 1;
sort(nums.begin(), nums.end());
for (i = 1; i <= target; ++i) {
  dp[i] = 0;
  for (auto& e : nums) { // 以每张纸币结尾的数量
    if (i - e >= 0 && dp[i - e] < INT_MAX - dp[i])
      dp[i] += dp[i - e];  // dp[i-e]<INT_MAX-dp[i]严卡题意，太过厉害的判断条件
    else
      break;
  }
}

丢鸡蛋

\(k\)个鸡蛋\(n\)层楼，鸡蛋恰好不碎的最小实验次数，题目链接。

  1. dp[k][n] \(k\)个鸡蛋\(n\)层楼的最小实验次数，状态转移方程

    1
    2
    for i in range(1, n+1):
    res=min(res, max(dp(k-1, i-1), dp(k, n-i))+1)

    base case：

    1
    2
    if k==1 return n
    if N==0 return 0

  2. 在上述方法中，因为dp(k, n)若\(k\)是定值，\(n\)是变量，则函数是单调的，因此可以使用二分查找最佳i的位置

  3. 重新定义状态dp[k][m] \(k\)个鸡蛋，最多扔\(m\)次可以检查到的最高楼层，状态转移思路如下，当随便找个楼层扔下一个鸡蛋：

    若鸡蛋碎了，还能测出来的最高的楼高为dp[k-1][m-1]

    若鸡蛋没有碎，还能测出来的最高楼高为dp[k][m-1]

    再加上扔的这一层，一共就是如下的状态转移方程：

    1
    dp[k][m]=dp[k-1][m-1]+dp[k][m-1]+1 # 注意是相加的关系

    base case：

    1
    2
    dp[0][:]=0
    dp[:][0]=0

戳气球

戳气球，一排气球，每个都有一个值，打破一个气球可以获得该气球以及左右两边气球的乘积分数。是一道经典动态规划问题。

定义状态dp[i][j]为打破\((i, j)\)气球，同时气球\(i\)和\(j\)还在时候的最大得分。在原来的气球序列的两侧添加上值为1的两个虚拟气球，dp[0][n+1]就是最终的答案，状态转移方程：

1
2
for k in range(i+1, j):  # 枚举最后打破的位置k
  dp[i][j]= max(dp[i][j], dp[i][k]+dp[k+1][j]+dp[i]*dp[j]*dp[k])

石子游戏

经典的博弈类型的游戏。

V1版本：N堆石头排成一列，小红和小黑轮流从两边取，取到石子数量最多的选手获胜，判断先手是否能赢。

动态规划：dp[i][j] 表示剩下石子堆i到j时，开始选的选手能拿到的最大分。最后判断dp[0][n-1]是否大于石子总数的一半。

V2版本：N堆石头排成一列，小红和小黑轮流从左边开始取X堆，X满足\(1 <= X <= 2M\)，同时更新M为\(max(M, X)\)。

动态规划：dp[i][m]表示剩下[i:]堆石头的时候，M为m值的时候，开始选的选手能拿到的最高分数。

V3版本，相比于V2版本，固定了M的值为3

V4版本，N堆石头排成一列，小红和小黑轮流从左边开始取X堆，X是一个非零的平方数，最后没有可取石子的人输掉游戏，判断先手是否能赢

V5版本，N堆石头排成一列，小红将其分成两列，小黑判断两列的石子总数，若总数不相同，则去掉数量大的那列，并且记这轮小红获得了剩下那列的总和，若数量相等，则让小红判断舍弃哪列。

V6版本，N堆石头，小红和小黑对每堆石头的价值的评价不同，他们互相知晓对方的评价标准，他们轮流取石头，最后按照自己的价值标准计算总价值，总量最大的获胜。

贪心：若有两堆石头，小红的评价是\(a_0\)、\(a_1\)，小黑的评价是\(b_0\)、\(b_1\)。先手拿第0堆他们之间的差值是a0-b1，若选第1堆的差值是a1-b0

V7版本，N堆石头排成一行，小红和小黑每次从左边或者右边选出一堆，剩下石头的总数就是该选手本轮的得分，计算后手与先手之间的最小差距。

V8版本，N推石头排成一行，小红小黑每次从左边取出X（x>1）个石头，取不出来则停止，获得这X个石头的所有价值Y，同时放回一个等于Y价值的石头在最左边，计算先后手之间差距。

动态规划：dp[i]在原始石头序列是i的情况下，要选选手和对方之间的最优。

Nim游戏，每个人可以拿走1～N个石子，拿到最后一个石子的人获胜，在总有N个石子的情况下，谁可以获胜？

屠龙勇士

勇士从矩阵的左上角出发去右下角拯救公主，经过每个网格勇士的血量都会发生变化，勇士只会向右或者向下走。需要血量始终大于等于1。

动态规划：反向思考，每个网格到右下角网格需要的最少血量，从右下角向左上角遍历。

打家劫舍

买卖股票

一只股票已知其每天的价格，按照买入、卖出依次进行的顺序（最多进行k次），计算能获得到的最大价值

动态规划：dp[i][k][0/1] 第\(i\)天的时候，在第\(k\)次交易情况下持有/不持有的最大收益。天数和次数都需要额外多一。

初始化的状态是：所有的未持有是0， 持有是INT_MIN。

状态转移方程

1
2
3
4
5
6
7
8
9
// 不持有, from {本次未持有， 本次卖出};   first表示未持有，second表示持有
dp[i][j].first = max(
  dp[i - 1][j].first, 
  dp[i - 1][j].second + prices[i - 1]);

// 持有, from {本次持有， 从上次买入}
dp[i][j].second = max(
  dp[i - 1][j].second, 
  dp[i - 1][j - 1].first - prices[i - 1]);

最长公共节点子序列

回溯

数独

子集

全排列

有效括号

贪心

最长递增子序列

最长递增子序列是贪心和二分的完美应用，有如下经典的变形题目

套娃信封，不同大小的信封，只有长度和宽度都比对方大，才能将对方放得下，问最多可以套娃多少个信封。

贪心的思想，先根据宽度从小到大将信封排列，宽度相同的，按照高度从大到小排列。我们期望的是从排好序的数组中一个一个的往外套从而找到最长的序列。

那么只要信封A比信封B（B在前，A在后）高，那么A一定可以装的下B。问题就变成了只看高度的最长递增子序列

无重叠区间、最少的箭引爆气球，这两个题的本质是一样的，都是找出最长的无重叠区间。

线段可以理解是一个点的拓展版。最长递增子序列的思想体现在相同长度的子序列长度，右侧占用的距离最小。

加油站良好出发点

一个环形的m个加油站场地，每个站点可以加一定数量的油，并且到下一个站点需要消耗一定数量的油，返回一个可以走完所有的加油站的出发点。

构造每个站点的盈余情况，即站点可以加的油减掉到下个加油站需要的油。

随便选择一个盈余大于等于0的站点出发，记录到这个站点时可以剩余的油left和可以从start来到这个站点需要的油量need；

依靠left，尽可能的向前行驶。

分治

数学相关

数字边界

计算器

有如下几种类型

加减乘除

只有一个数字栈，最终栈中的元素相加为最后的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int calculate(string s) {
  char sign = '+'; int num = 0, a;
  stack<int> sta;
  int index = 0;
  for (char c : s) {
    if (isdigit(c)) num = num * 10 + (c - '0');
    if ((!isdigit(c) && c != ' ') || index == s.size() - 1) {
      if (sign == '+') sta.push(num);
      else if (sign == '-') sta.push(-num);
      else if (sign == '*' || sign == '/') {
        a = sta.top(); sta.pop();
        if (sign == '*') sta.push(a * num);
        else sta.push(a / num);
      }
      sign = c, num = 0;
    }
    ++index;
  }
  num = 0;
  do {
    num += sta.top();
    sta.pop();
  } while (!sta.empty());
  return num;
}

位运算

大数相乘

大数相乘，若结果过大应该对1e9+7取模。将乘法分解 \[ \begin{array}{l}(a * b) \equiv m \\ =\left(\sum b * a_{i}\right) \equiv m, \ \ a=\sum a_{0}+a_{1}+\cdots+a_{r} \\ =\sum (b * a_{i}) \equiv m\end{array} \] 我们可以将a拆解成如下部分 \[ a=x_{0} * 2^{0}+x_{1} * 2^{1}+x_{n} * 2^{n}, x_{i} \in\{0,1\} \\ x_{i}=\frac{a}{2^{i}} \% 2 \] 程序实现

1
2
3
4
5
6
7
8
long long m(long long a, long long b) { // 大数相乘
  long long res = 0, temp = a;
  while (b) {
    if (b % 2) res += temp, res %= mod;
    b >>= 1, temp <<= 1, temp %= mod;
  }
  return res;
}

最大公约数

1
2
3
4
5
int gcd(int x, int y) {
  return (y != 0) ? gcd(y, x % y) : x;
}
g = gcd(x, y); // 最大公约数
gy = a * b / g; // 最小公倍数

阶乘

快速幂

通过二进制的方式快速的计算幂

开平方

通过牛顿法开平方。每次迭代的目标是从\(x_i\)的位置推导出\(x_{i+1}\)的位置。

1
2
3
4
5
6
7
8
9
10
11
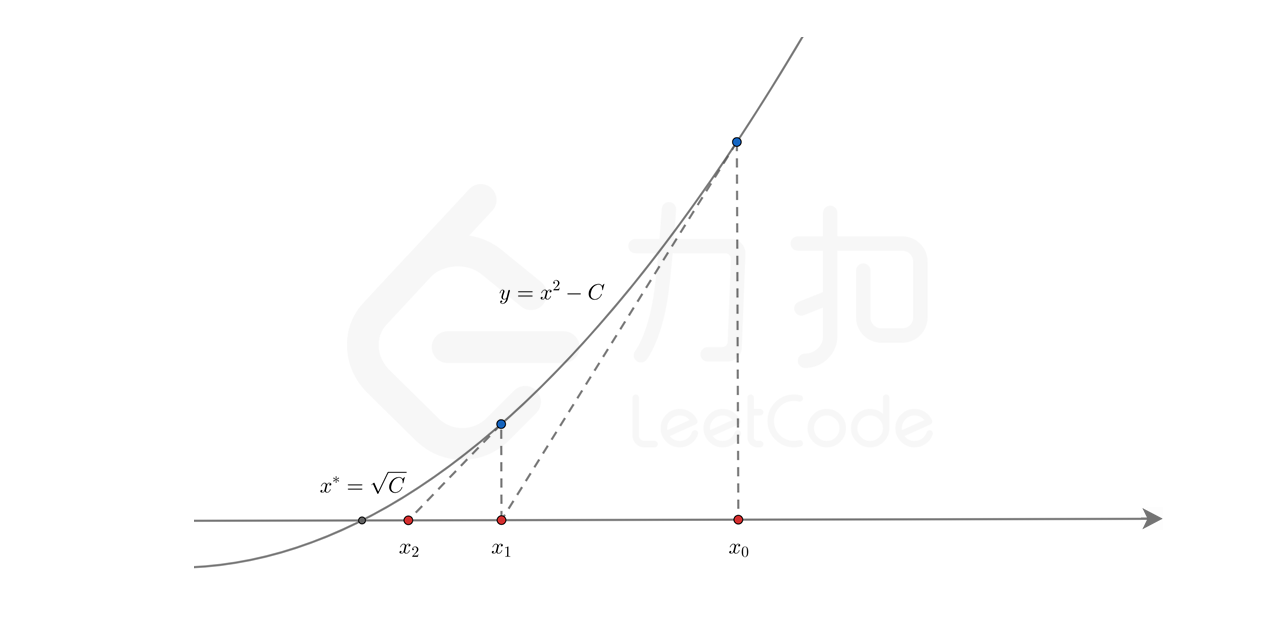
12
int mySqrt(int x) {
  if (x == 0) return 0; // 防止除0
  double c = x, x0 = x; // 从x开始初始化，防止找到了负数
  while (true) {
    double xi = 0.5 * (x0 + c / x0); // 导数的斜线与x轴的交点;除法需要进行判断
    if (fabs(x0 - xi) < 1e-7) {
      break;
    }
    x0 = xi;
  }
  return int(x0);
}

进制转换

等概率

Rand

类似于用 Rand7() 实现 Rand10()，用小的rand数生成大的rand数

  1. 拒绝采样，rand7，通过两次调用，可以生成0-49个随机数，砍掉不满10个数的部分
  2. 在拒绝采样的部分，继续测试
  3. 进制来实现

蓄水池算法

题目类似于链表随机节点，在长度很长且未知的数据流中随机采样x个数字。

思路是：每个数被最终选中的概率都是被选中的概率 * 不被替换的概率，伪代码如下。

1
2
3
4
5
6
7
8
9
10
11
vector<int> calc(vector<int> arr, int k) {
  vector<int> ans(arr.begin(), arr.begin() + k);
  int i = k, n = arr.size(), j;
  for (;i < n;++i) {
    j = rand() % (i + 1));
    if (j < k) {
      ans[j] = arr[i];
    }
  }
  return ans;
}

可以举个例子，5个元素，随机保留3个，则

1 2 3 4 5
被选中 \(1\) \(1\) \(1\) \(\frac{3}{4}\) \(\frac{3}{5}\)
不被替换 \(\frac{3}{4} * \frac{4}{5}\) \(\frac{3}{4} * \frac{4}{5}\) \(\frac{3}{4} * \frac{4}{5}\) \(\frac{4}{5}\) \(1\)
保留 \(\frac{3}{5}\) \(\frac{3}{5}\) \(\frac{3}{5}\) \(\frac{3}{5}\) \(\frac{3}{5}\)

洗牌

  • 逐次随机抽取

    随机抽取一张牌，直到抽出所有的牌就是最终的洗牌结果

  • 多次随机交换

    随机抽两张牌进行交换，抽的次数足够多就完成了洗牌

  • Fisher–Yates shuffle算法

    每次随机选取一个数，然后将该数与数组中最后(或最前)的元素相交换(如果随机选中的是最后/最前的元素，则相当于没有发生交换)；然后缩小选取数组的范围，去掉最后的元素,即之前随机抽取出的数。重复上面的过程，直到剩余数组的大小为1，即只有一个元素时结束。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    void shuffle(int* array, int len) {
      int i = len;
      int j = 0;

      while (--i > 0) {
        j = rand() % (i + 1);
        swap(array[i], array[j]);
      }
    }

数学技巧

可怜的小猪

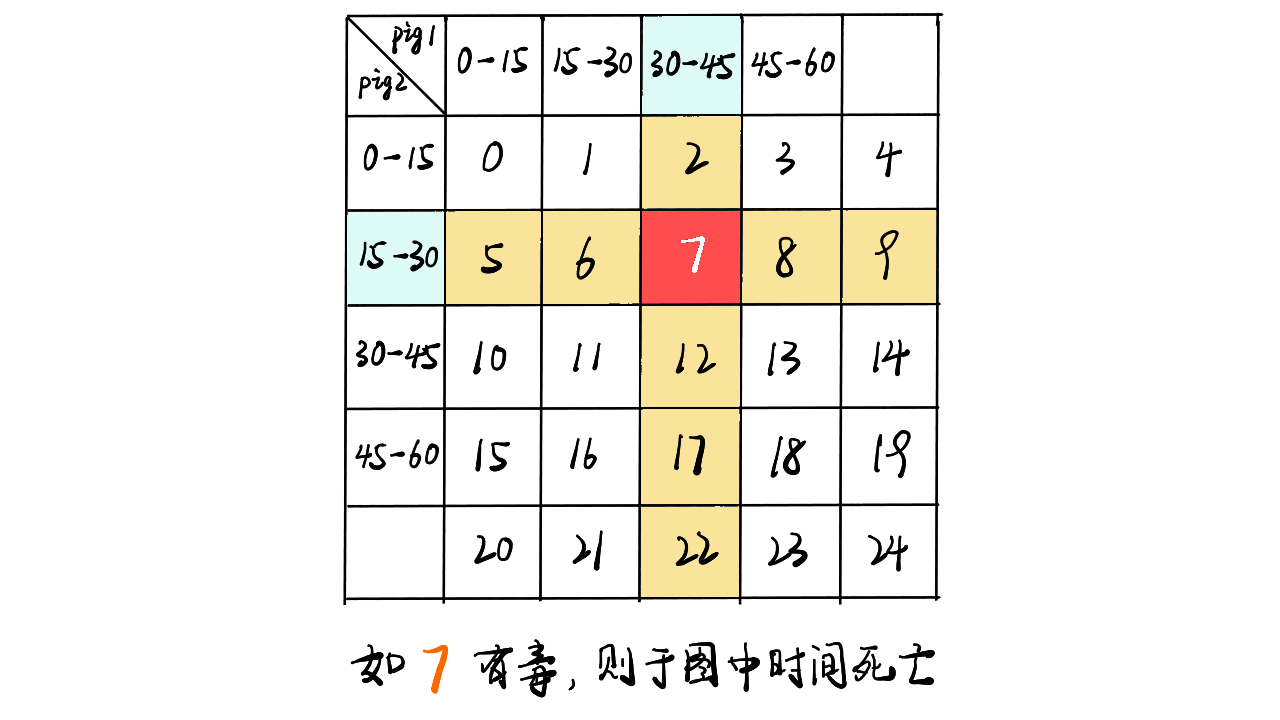
可怜的小猪，给小猪喝液体x分钟的时候，会知道液体是否是毒药。bucket桶液体，总共sum分钟的时间，要找到时毒药的液体（只有一瓶）

可知一共可以经过\(times=sum/x\)次数的测试，每只猪会有\(status=times+1\)次的状态，例如可以测3次的时候，可以有如下的状态。

D
AD
AAD
AAA

那么两只猪的状态总数是\(status^2\)，类比正方体，同样的3只猪会是立方体，因此x只猪的状态总数是\(status^x\)。由此可知晓猪，次数以及可以测试的液体份数。

图片参考链接