算法的基础知识积累

基本算术

求平均值

给定一个long型数组，求数组的平均值。

首先为防止两个long相加越界，可以采用先除再加的方法，保证了总和不会越界

\[ \frac{\sum_{i=0}^{n-1} \operatorname{arr}[i]}{n}=\sum_{i=0}^{n-1} \frac{\operatorname{arr}[i]}{n} \]

不能采用浮点数的方案，因为浮点数的精度损失是不可控的，所以应该选择使用余数来收集小数部分 \[ \sum_{i=0}^{n-1} \frac{\operatorname{arr}[i]}{n}=\sum_{i=0}^{n-1} \operatorname{long}\left(\frac{\operatorname{arr}[i]}{n}\right)+\frac{\sum_{i=0}^{n-1} \operatorname{arr}[i] \%(n)}{n} \]

但是这还有一个问题，余数部分的相加仍有越界的风险，在实际计算的过程中，应该累加到大于等于n或者小于等于-n之后，就累加一个1或者-1给最终的结果

long get_avg(long* arr, long length){
    long MLONG_MAX = length;
    long MLONG_MIN = -MLONG_MAX;
    long ans=0;
    long mod=0;
    long x;
    for(long i=0;i<length;++i){
        ans+=arr[i]/length;
        x=arr[i]%length;
        if(x+mod>=MLONG_MAX){
            ans++;
            mod=mod-MLONG_MAX+x;
        }else if(x+mod<=MLONG_MIN){
            ans--;
            mod=x-MLONG_MIN+mod;
        }else{
            mod+=x;
        }
    }
    return ans+mod/length;
}

备注：C++中的负数取余计算逻辑

int main(void){
	int i;
	for(i=-4;i<=4;++i) cout<<i<<" "<<(i%3)<<endl;
	return 0;
}
// -4 -1
// -3 0
// -2 -2
// -1 -1
// 0 0
// 1 1
// 2 2
// 3 0
// 4 1

大数相乘

大数相乘，若结果过大应该对1e9+7取模。将乘法分解 \[ \begin{array}{l}(a * b) \equiv m \\ =\left(\sum b * a_{i}\right) \equiv m, \ \ a=\sum a_{0}+a_{1}+\cdots+a_{r} \\ =\sum (b * a_{i}) \equiv m\end{array} \] 我们可以将a拆解成如下部分 \[ a=x_{0} * 2^{0}+x_{1} * 2^{1}+x_{n} * 2^{n}, x_{i} \in\{0,1\} \\ x_{i}=\frac{a}{2^{i}} \% 2 \] 程序实现

long long m(long long a, long long b){ // 大数相乘
  long long res=0, temp=a;
  while(b){
    if(b%2) res+=temp, res%=mod;
    b>>=1, temp<<=1, temp%=mod;
  }
  return res;
}

南航机试常用方法与技巧

日期的处理

判断某个年份是不是闰年

1
2
3

bool ISYEAP(int x){
  return x%4==0&&(x%100!=0||x%400==0); // 4的倍数且如果是100的倍数，只能是400的倍数
}

计算两个日期之间的差值的思想：记录所有天数到元年的天数差

二分查找

// 在一个数组中查找某个数
int binsearch(int low, int hight, int tar, int arr[]){
  int mid;
  while(low<=high){
    mid=(low+high)>>1;
    if(arr[mid]>tar) high=mid-1;
    else if(arr[mid]<tar) low=mid+1;
    else return mid;
  }
  return -1;
}
// todo 正确性待定
// 查找某个数在数组中的段（左闭右开）
// 可以理解是二分查找第一个比tar大于等于位置的下标（不包含数组最后一个元素的下标）
int segsearch(int low, int high, int tar, int arr[]){
  if(tar<arr[low]||tar>arr[high]) return -1;
	int mid;
  while(low<high-1){
    mid=(low+high)>>1;
    if(arr[mid]>tar) high=mid;
    else if(arr[mid]<tar) low=mid;
    else return mid;
  }
  return low;
}

属性数值

最大公约数 & 最小公倍数

最大公约数：两个整数共有约数最大的一个

最小公倍数：两个整数共有倍数最大的一个

int gcd(int x, int y){
  return (y != 0)?gcd(y, x%y) : x;
}
g=gcd(x, y); // 最大公约数
gy=a*b/g; // 最小公倍数

大整数求余

定义a,b和m ，若满足(a-b)/m为整数，那么就称a和b对模m同余，计作 \[ \mathrm{a} \equiv \mathrm{b}(\mathrm{mod} \ \mathrm{m}) \] 对模m同余是整数的一个等价关系。

// 基于等价关系，对大数求余数
int modBigNum(string s, int mod){
  int i, flag=0;
  for(i=0;i<s.size();++i) flag=(flag*10+(s[i]-'0'))%mod;
  return flag;
}

素数

只能被1和它自身整除的数

对于n，对2到sqrt(n)的整数分别测试是否可被整除即可。

哈夫曼树

利用小根堆，每次取权重最小的两个节点，合并成一个新的节点，该节点的权重为两个叶子结点的权重只和，直到小根堆中只有一个节点。(先合并的节点的深度更可能会比较的深)

并查集

const int N=10008;
int a[N];
void init(){memset(a, N, -1);}
int findr(int x){if(a[x]<0)return x;return a[x]=findr(x);}
void merge(int x,int y){
    x=findr(x),y=findr(y);
    if(x!=y)a[x]=y;
}

Github

排序算法

排序算法	平均时间复杂度	最差时间复杂度	空间复杂度	数据对象稳定性
冒泡排序	O(n2)	O(n2)	O(1)	稳定
选择排序	O(n2)	O(n2)	O(1)	数组不稳定、链表稳定
插入排序	O(n2)	O(n2)	O(1)	稳定
快速排序	O(n*log2n)	O(n2)	O(log2n)	不稳定
堆排序	O(n*log2n)	O(n*log2n)	O(1)	不稳定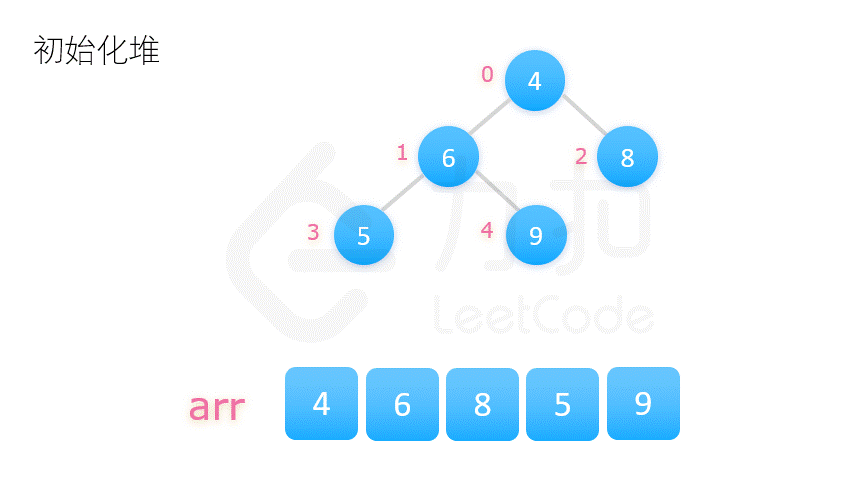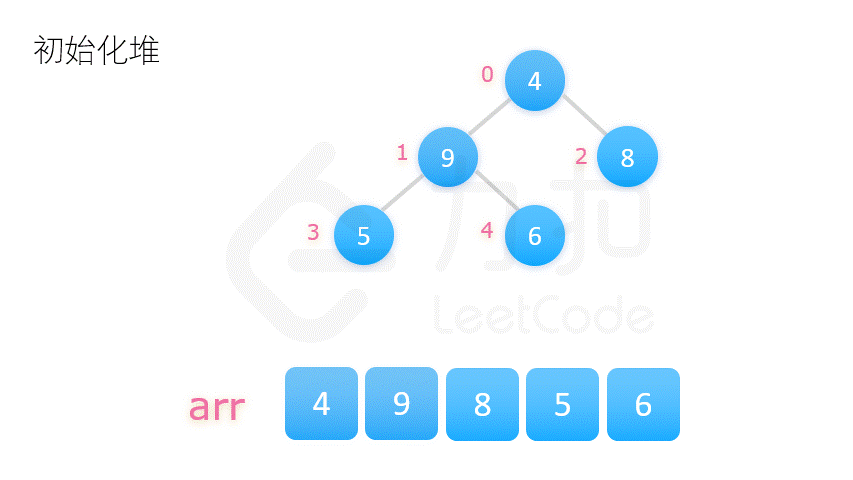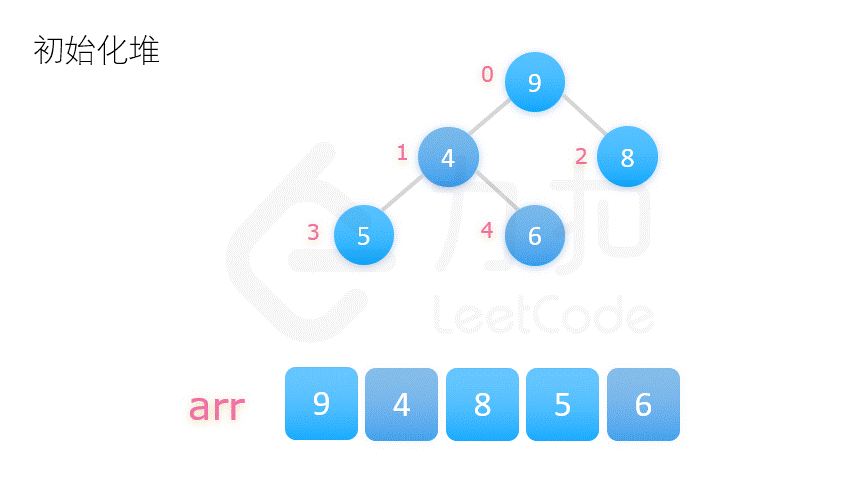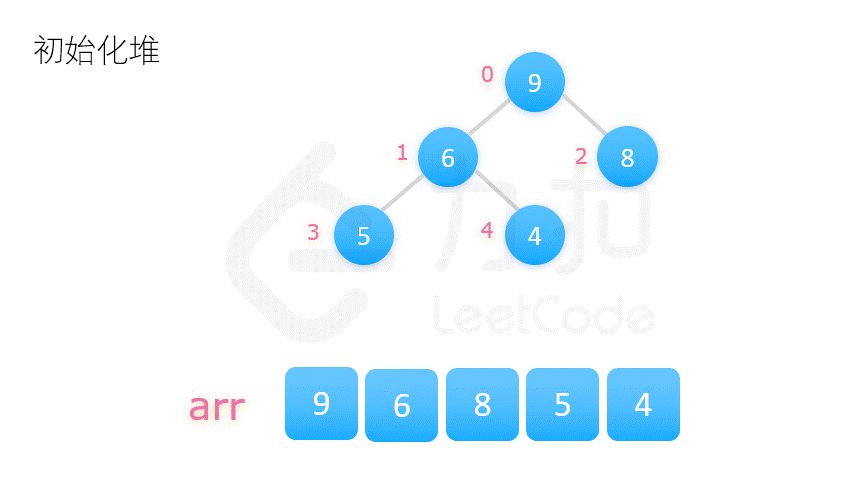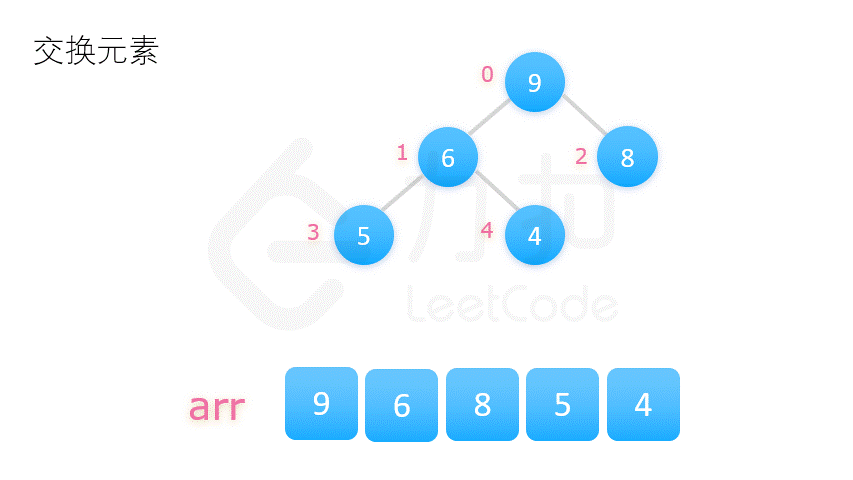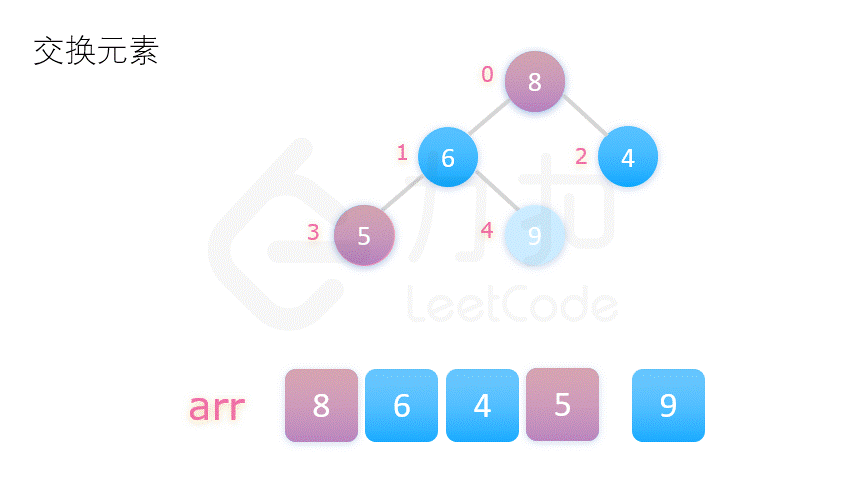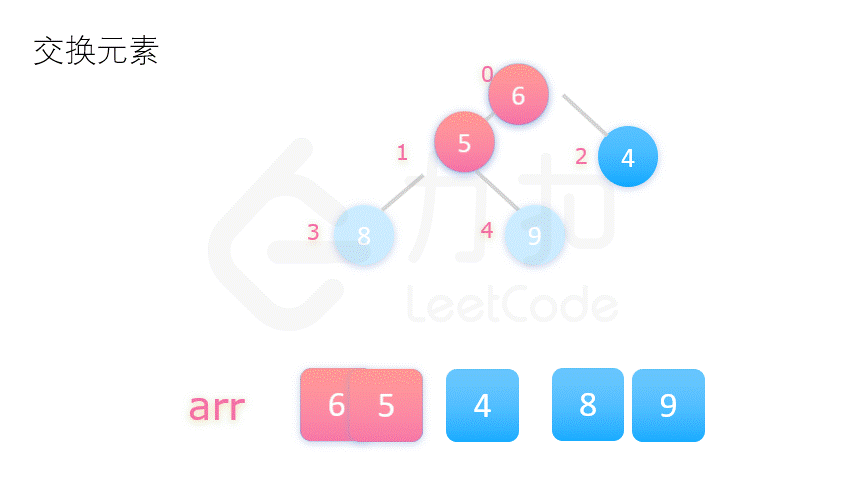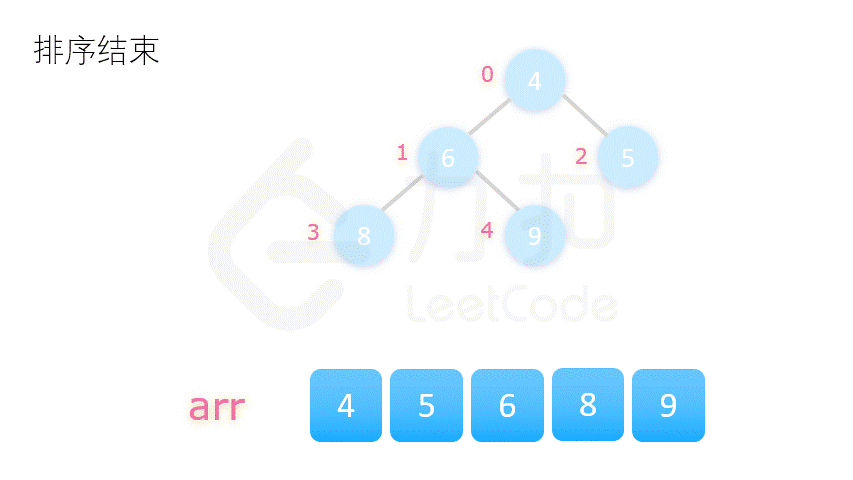
归并排序	O(n*log2n)	O(n*log2n)	O(n)	稳定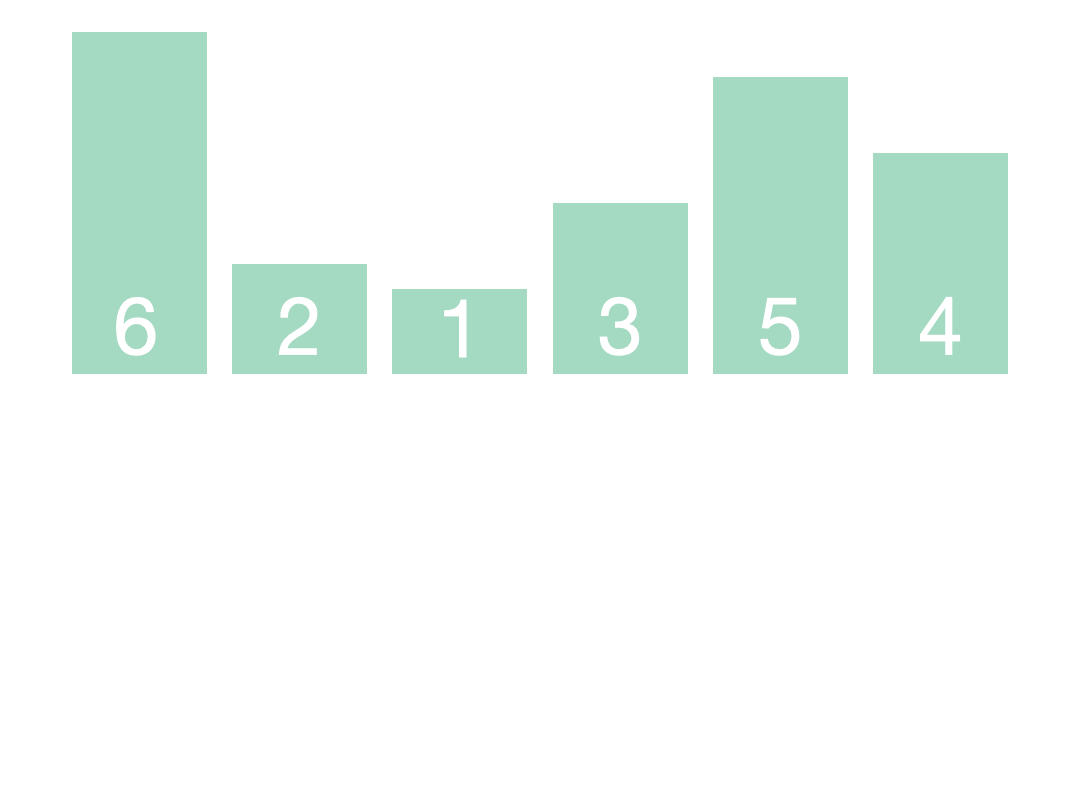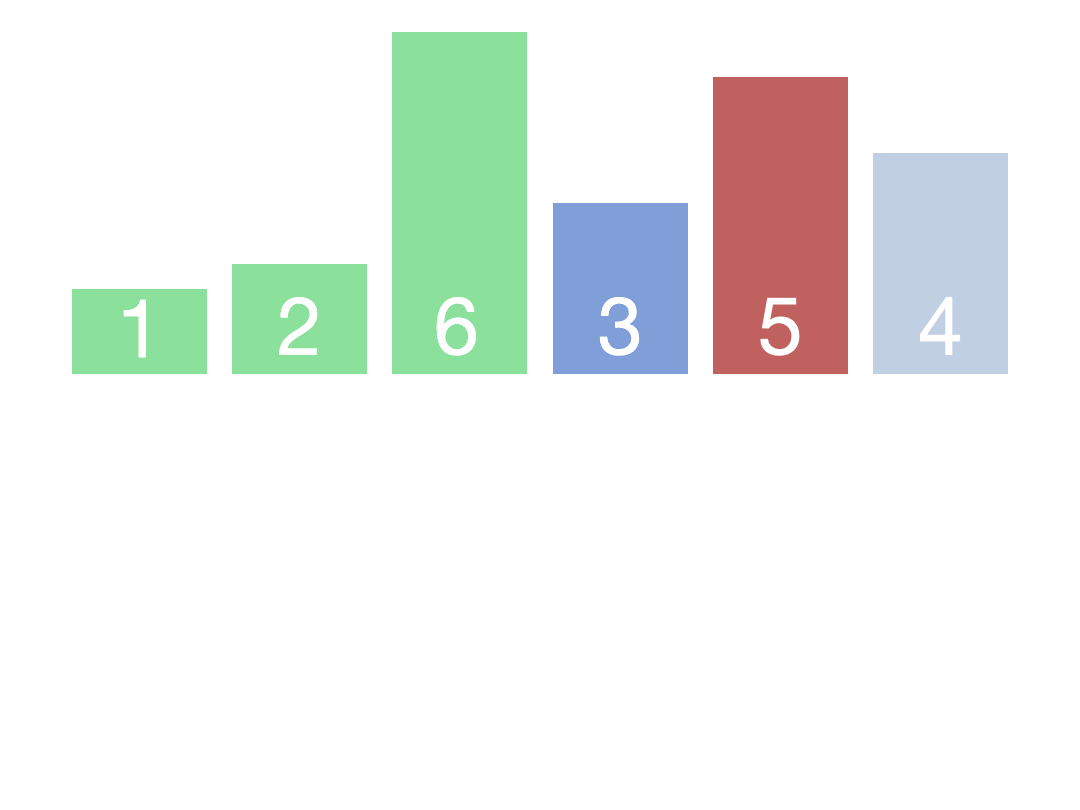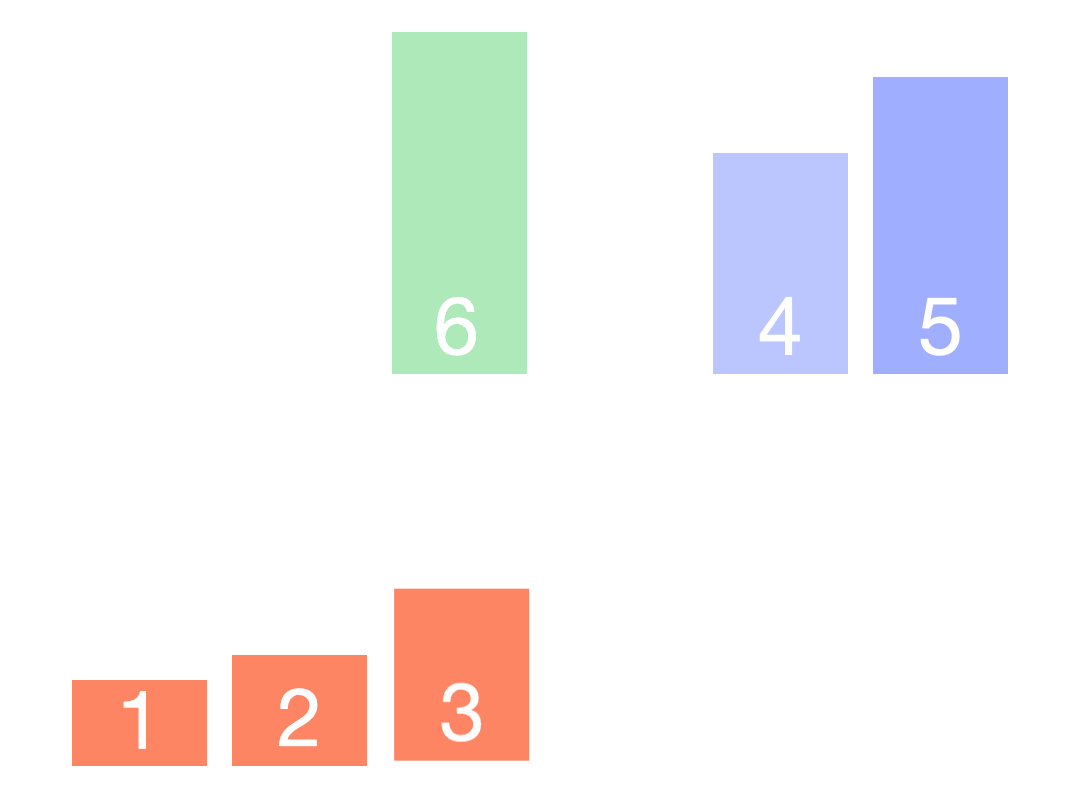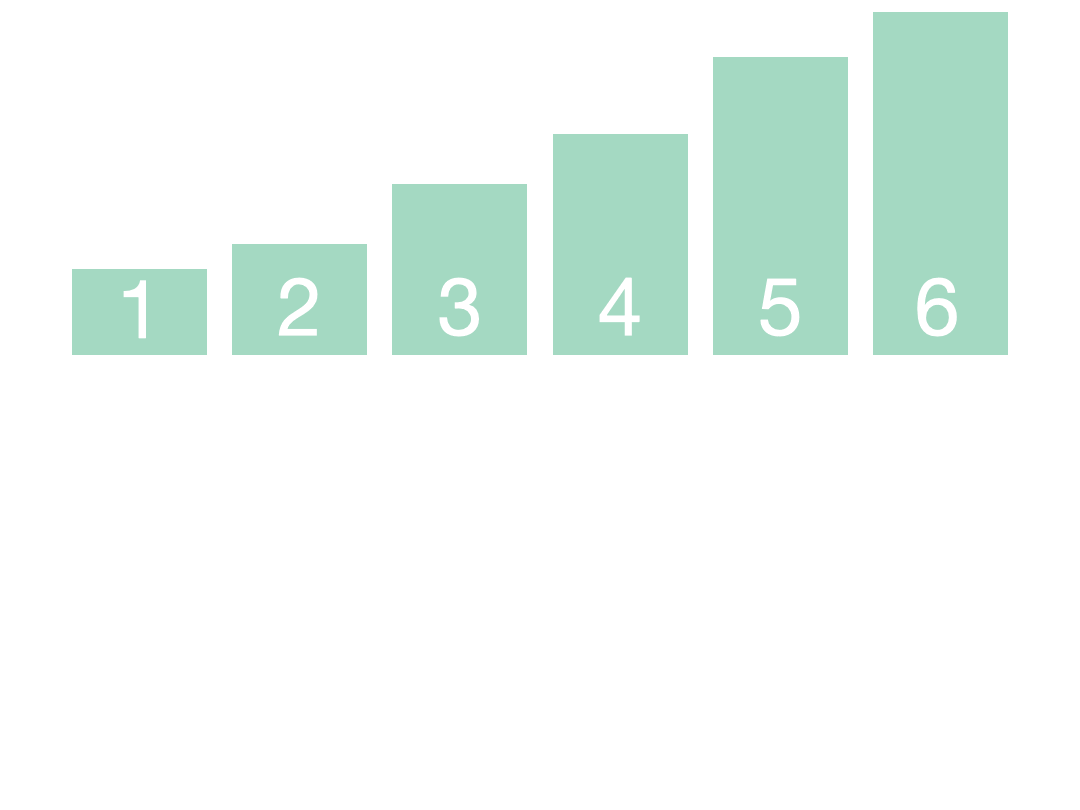
希尔排序	O(n*log2n)	O(n2)	O(1)	不稳定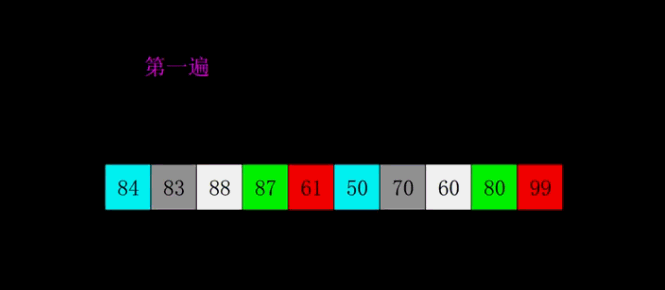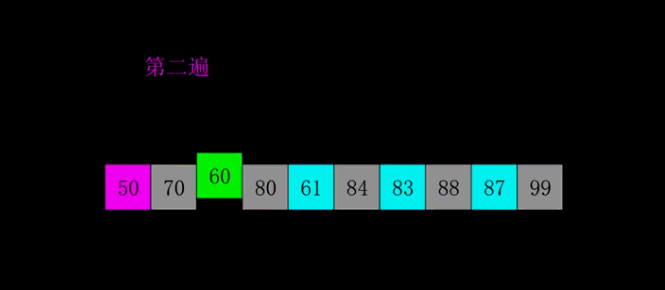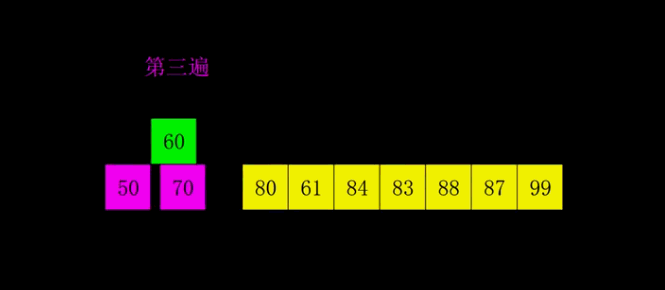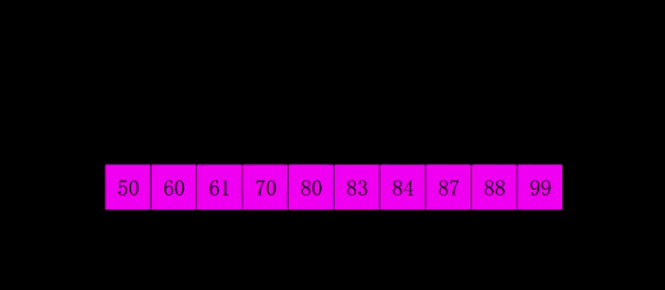
计数排序	O(n+m)	O(n+m)	O(n+m)	稳定
桶排序	O(n)	O(n)	O(m)	稳定
基数排序	O(k*n)	O(n2)		稳定