《STL源码剖析》读书笔记

新年快乐！希望大家牛年一切顺利！

STL综述

STL组成

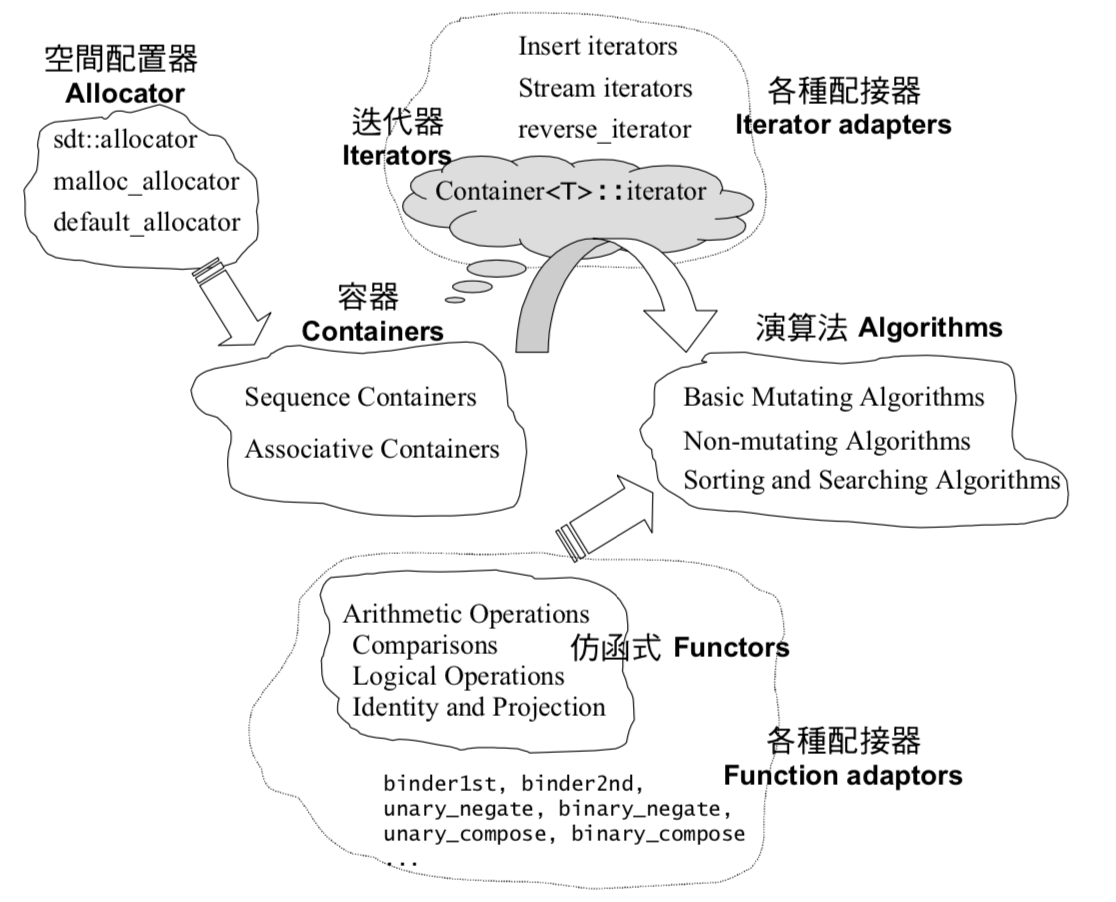
STL由如下六部分共同组成，但我平时了解接触最做的只是容器与迭代器，对其他东西的了解都十分浅薄（其实就是nothing！）。

• Allocator：空间配置器
• Containers：容器
• Iterators：迭代器
• Algorithms：算法
• Functors：仿函数
• Adapter：配接器

Container通过Allocator取得数据存储空间，Algorithm通过Iterator存取Container内容，Functor协助Algorithm完成不同的策略变化，Adapter可以修饰Container、functor和iterator等等，起到一个连接、套接的功能。

关于头文件

STL的所有的头文件大概可以分为5组

• C++标准规范下的C头文件（无扩展名）例如cstdio, cstring...
• C++标准程序库中不属于STL范畴者，例如stream, string...相关文件
• STL标准头文件（无扩展名）例如vector, deque, list等
• C++ standard定案前，所规范的STL头文件，例如vector.h, deque.h, list.h等
• SGI STL内部文件（STL真正被实现的地方），例如stl_vector.h, stl_deque.h等

具体内容

Allocator

空间配置器的标准接口有如下几种：

接口	含义
allocator::value_type	迭代器所指对象的型别
allocator::pointer	允许通过指针改变对象的内容，返回的是T&
allocator::const_pointer	允许通过指针改变对象的内容，返回的是const T&
allocator::reference	返回值可以赋值，返回的是左值
allocator::const_reference	返回值不可以被赋值
allocator::size_type
allocator::difference_type	用来表示两个迭代器之间的距离
allocator::rebind
allocator::allocator()
allocator::allocator(const allocator&)
template allocator::allocator(const allocator&)	泛化的构造函数
allocator::~allocator()
pointer allocator::address(reference x) const	返回某个对象的地址，同于&x
const_pointer allocator::address(const_reference x) const	返回某个const对象的地址，同于&x
pointer allocator::allocate(size_type n, const void* = 0)	配置空间，足以存储n个T对象， 第二个参数可能会利用它来增进区域性
void allocator::deallocate(pointer p, size_type n)	归还先前配置的空间
size_type allocator::max_size() const;	返回可成功配置的最大量
void allocator::construct(pointer p, const T& x)	等同于 new ((void *) p) T(x)
void allocator::destroy(pointer p)	等同于p->~T()

内存配置::operator new()，相当于c语言中的malloc()

内存释放::operator delete()，相当于c语言中的free()

构造和析构工具

• 构造函数construct

  template <class T1, class T2>
  inline void construct(T1* p, const T2& value){
    new (p) T1(value); // 将初值设置到指针所指的空间上
  }

• 析构函数destroy，有两个版本

  • 第一版本，接受一个指针，执行指针的析构函数
  • 第二个版本，接受一个first指针和一个last指针，删除[first, last)范围内的数据，并判断具体型别的析构函数是否有实际意义，若有实际意义才会调用析构函数，否则直接退出。

空间的配置与释放

• 设计思想
  • 向system heap要求空间
  • 考虑多线程状态
  • 考虑内存不足时的应变策略
  • 考虑过多“小型区块”可能造成的内存碎片（fragment）问题
• 空间配置，有两级配置器，处理内存碎片的问题
  • 第一级配置器__malloc_alloc_template，直接调用alloc()或者realloc()，失败后会调用oom_(re)alloc尝试达到目的（需要客户端设定内存不足处理例程）
  • 第二级配置器__default_alloc_template
    • 若区块够大，超过128bytes，就移交第一级配置器处理
    • 若区块较小，则以内存池管理。一次性申请一个大空间，动态分配、回收给用户使用。
      • 会主动将要申请的小额区块的内存上调至8的倍数。
      • 会维护16个free-lists，各自管理8*i bytes的小额区块
      • 当free_lists 资源不足时，会调用refill()函数重新填充，如果可以会分配20个单位，空间不足时会分配一个单位
      • refill()函数中实际内存调度是由chunk_alloc()函数完成
        • 检查内存池的空闲空间是否充足，充足的话，分配20个单位；不足20单位，但足一个单位就分配一个单位
        • 一个单位也不足时，向heap申请空间（malloc()），申请的空间大小为需要的2倍再加上一个随着申请heap频率增加而增加的额外数量
        • heap空间不足时，检查自身剩余的空间数量，尝试资源调整。（不会尝试向heap申请更小的空间，这种策略在多线程环境下会造成灾难）
• 空间释放
  • 若空间大小大于128，调用deallocate()函数
  • 若空间大小小于128，向free_lists归还空间
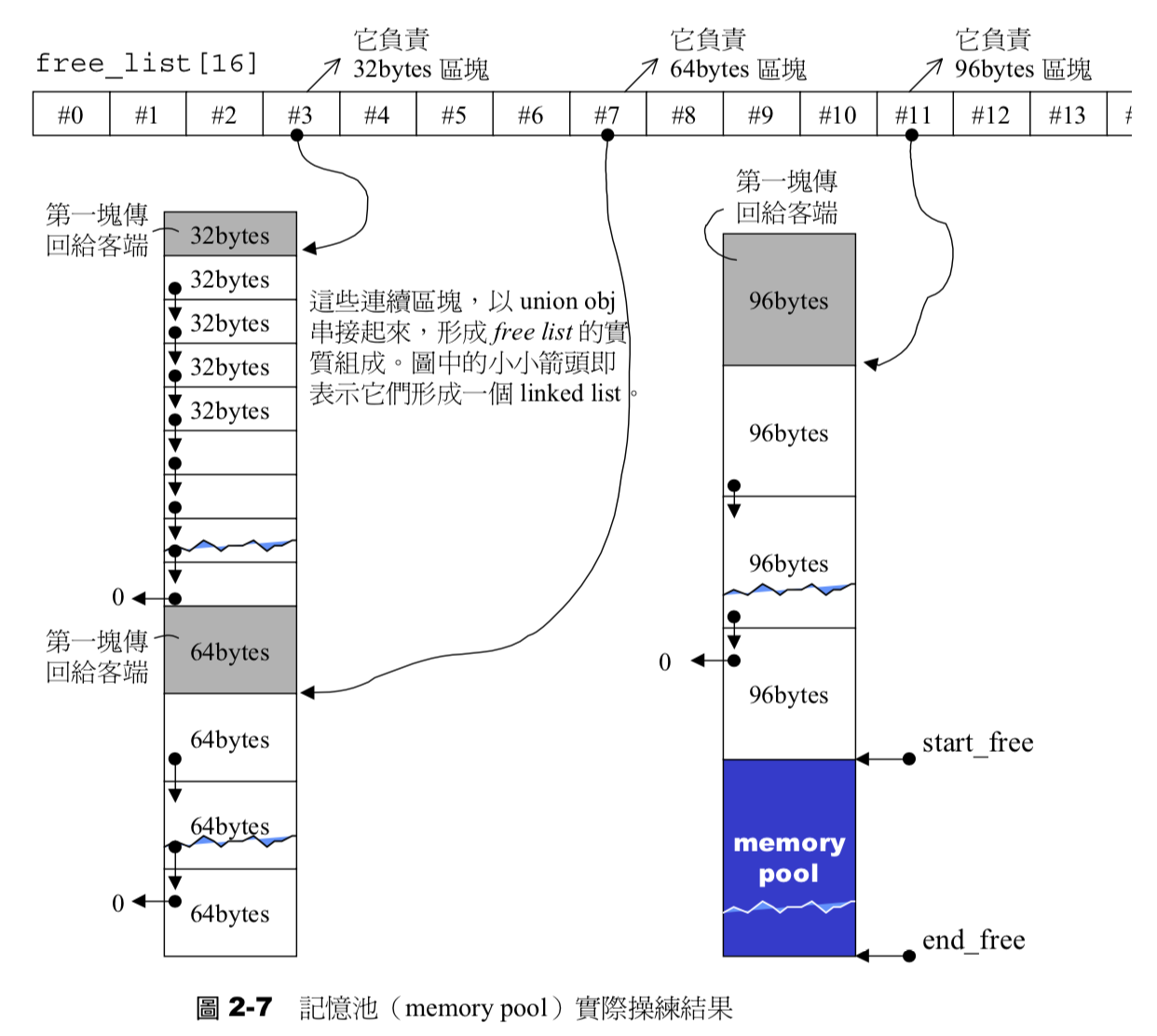
• 内存池管理逻辑图

内存基本处理工具

• uninitialized_copy，函数签名如下InputIterator 数据传入指针，ForwardIterator内存构造指针

  ForwardIterator uninitialized_copy(InputIterator first, InputIterator last, ForwardIterator result);
  // 在[first, last)范围中的每个迭代器i,实际调用
  construct(&*(result+(i-first)), *i)

• uninitialized_fill，在固定范围上复制x

  void uninitialized_fill(ForwardIterator first, ForwardIterator last, const T& x);
  // 实际调用
  construct(&*i, x);

• uninitialized_fill_n，从某个位置开始，复制x次

  inline uninitialized_fill_n(ForwardIterator first, Size n, const T& x);
  // 实际调用
  construct(&*i, x);

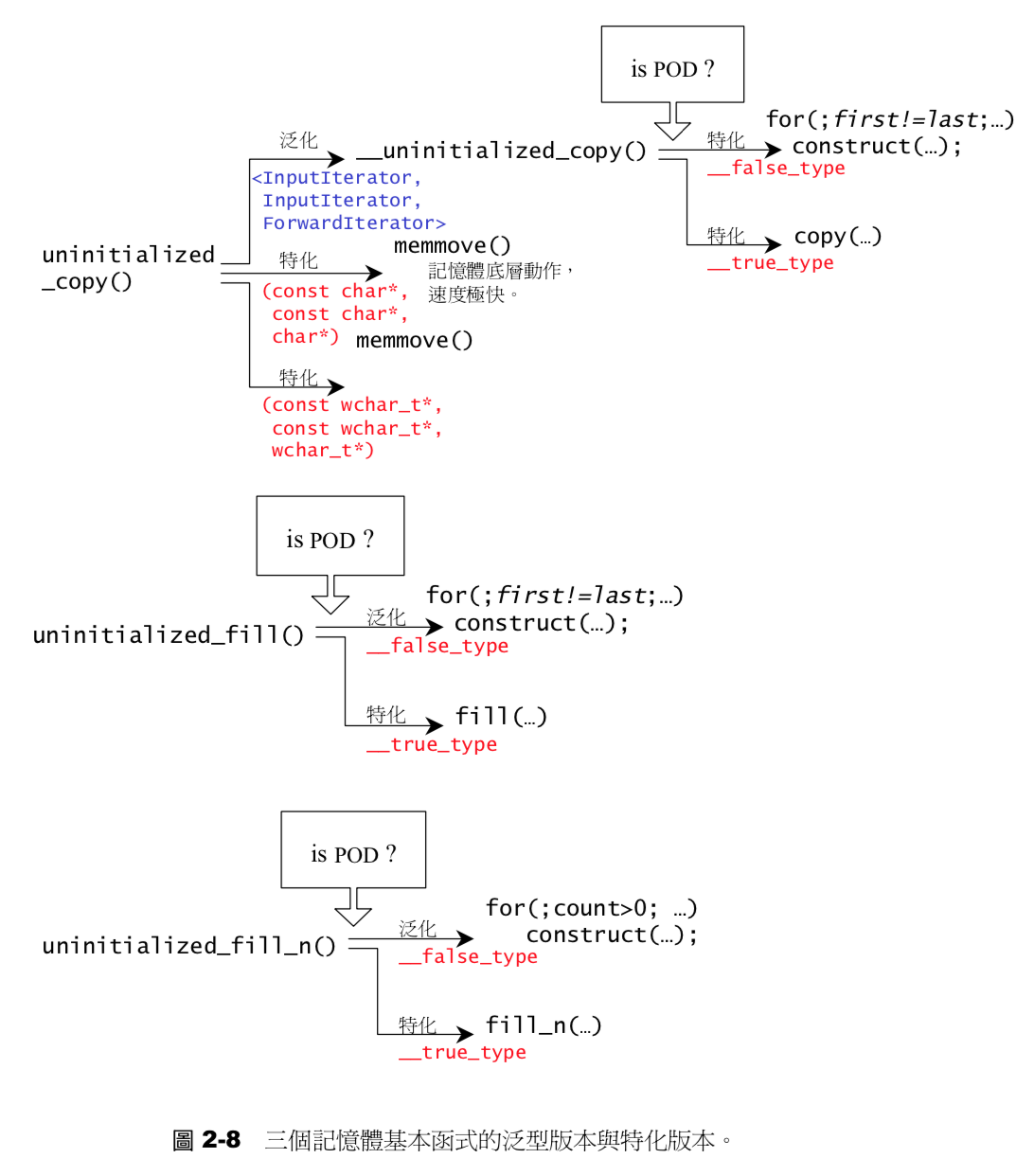
上述三个函数都会判断要构造的类型是否是POD(Plain Old Data)，即是否是标量型别（scalar type）或者是传统的C struct型别，最主要个的特点是其构造和析构都是不太重要的（trivial）的，可以使用fill函数进行内存填充。对于非POD类型会使用construct函数进行构造。流程如下图所示：

Iterator

迭代器--智能指针

iterator的本质是一种智能指针（smart pointer），最重要的是内容提领（dereference）和成员访问（member access），因此迭代器最重要的是对operator *和operator ->进行重载。书中包含了简化版本的auto_ptr实现。

template<class T>
class auto_ptr{
  public:
    explicit auto_ptr(T *p = 0) pointee(p) {}
    template<class U>
    auto_ptr(auto_ptr<U>& rhs): pointee(rhs.release()) {}
    ~auto_ptr() { delete pointee; }
    template<class U>
    auto_ptr<T>& operator=(auto_ptr<U>& rhs) {
      if(this != &rhs) reset(rhs.release());
      return *this;
    }
    T& operator*() const { return *pointee; }
    T* operator->() const { return pointee; }
    T* get() const { return pointee; }
    // ...
    // 针对list的iterator
    // 自增操作 ++ptr调用此函数
    auto_ptr& operator++() {
      pointee = pointee->next(); 
      return *this;
    }
    // 自增操作 ptr++调用此函数，默认会将一个0,传入给函数，来区分前置还是后置的++
    auto_ptr operator++(int) {
      auto_ptr tmp = *this;
      ++*this;
      return tmp;
    }
    bool operator==(const auto_ptr& other) {
      return pointee==other.pointee;
    }
    bool operator!=(const auto_ptr& other) {
      return pointee==other.pointee;
    }
  private:
    T *pointee;
}

获取迭代器的相应型别

关键代码

template <class I>
struct iterator_traits {
  typedef typename I::value_type value_type; // typename 告诉编译器把一个特殊的名字解释成类型
}
// 偏特化版本，针对原生指针
template <class T>
struct iterator_traits<T*> {
  typedef T value_type;
}
// 偏特化版本，针对pointer-to-const
template <class T>
struct iterator_traits<const T*> {
  typedef T value_type;
}

通过iterator_traits可以萃取迭代器所指对象的型别。

具体分为：

迭代器的型别	含义
value_type	迭代器所指内容的型别
difference_type	迭代器之间的距离
reference type & pointer type	迭代器所指内容是否可以被改变
迭代器类型	见下

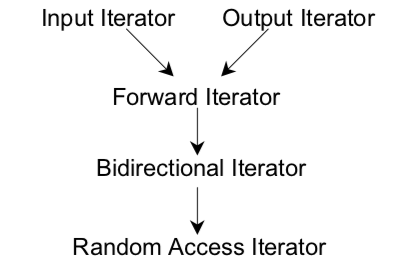
迭代器类型分为如下五种，特点如下：

• Input Iterator 只读类型，不允许被改变
• Output Iterator 只写
• Forward Iterator 允许在其指定的区间上读写
• Bidirectional Iterator 可以双向移动
• Random Access Iterator 可以自由移动比较

迭代器类型的应用

// 通过类名进行标记，有两个好处
// 1. 可以被重载函数当作参数使用
// 2. 若没有对应tag的函数，会自动向上找到tag的父类的重载函数进行调用
// Input Iterator 
struct input_iterator_tag {};
// Output Iterator 
struct output_iterator_tag {};
// Forward Iterator 
struct forward_iterator_tag : public input_iterator_tag {};
// Bidirectional Iterator 
struct bidirectional_iterator_tag : public forward_iterator_tag {};
// Random Access Iterator 
struct random_access_iterator_tag : public bidirectional_iterator_tag {};

// STL的命名规则，以算法能接受的最低阶迭代器类型，来为其迭代器型别参数命名
template<class Iterator, class Distance>
inline void advance(InputIterator& i, Distance n){
  __advance(i, n, iterator_traits<InputIterator>::iterator_category());
}

// 通过重载的方式，实现不同的指针执行不同的策略
template <class InputIterator, class Distance>
inline void __advance(InputIterator& i, Distance n, input_iterator_tag) {
  while(n--) ++i;
}

template <class InputIterator, class Distance>
inline void __advance(InputIterator& i, Distance n, bidirectional_iterator_tag) {
  if(n>=0) while(n--) ++i;
  else while(n++) --i;
}

此外迭代器还能够判断所指对象是不是不重要的构造和析构。实现的方式是人工来指定。

Sequence Container

根据数据在容器中的排列特性，将数据结构分为序列式和关联式两种，具体如下图所示。

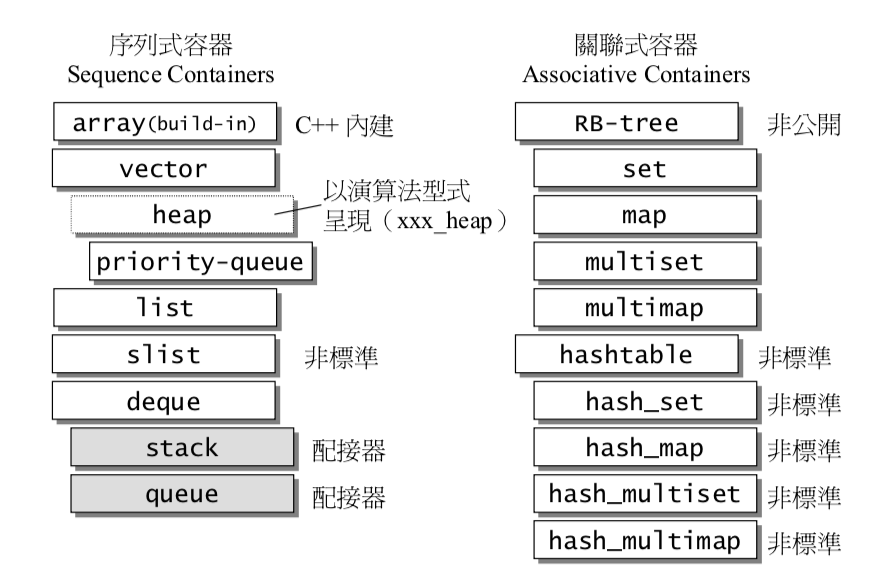
vector

• 使用顺序存储空间进行存储，迭代器直接为T*

• 不会主动释放空闲的存储空间，空间扩容需要经过申请新空间->数据拷贝->释放旧空间的步骤

• 设计示意如下图
  

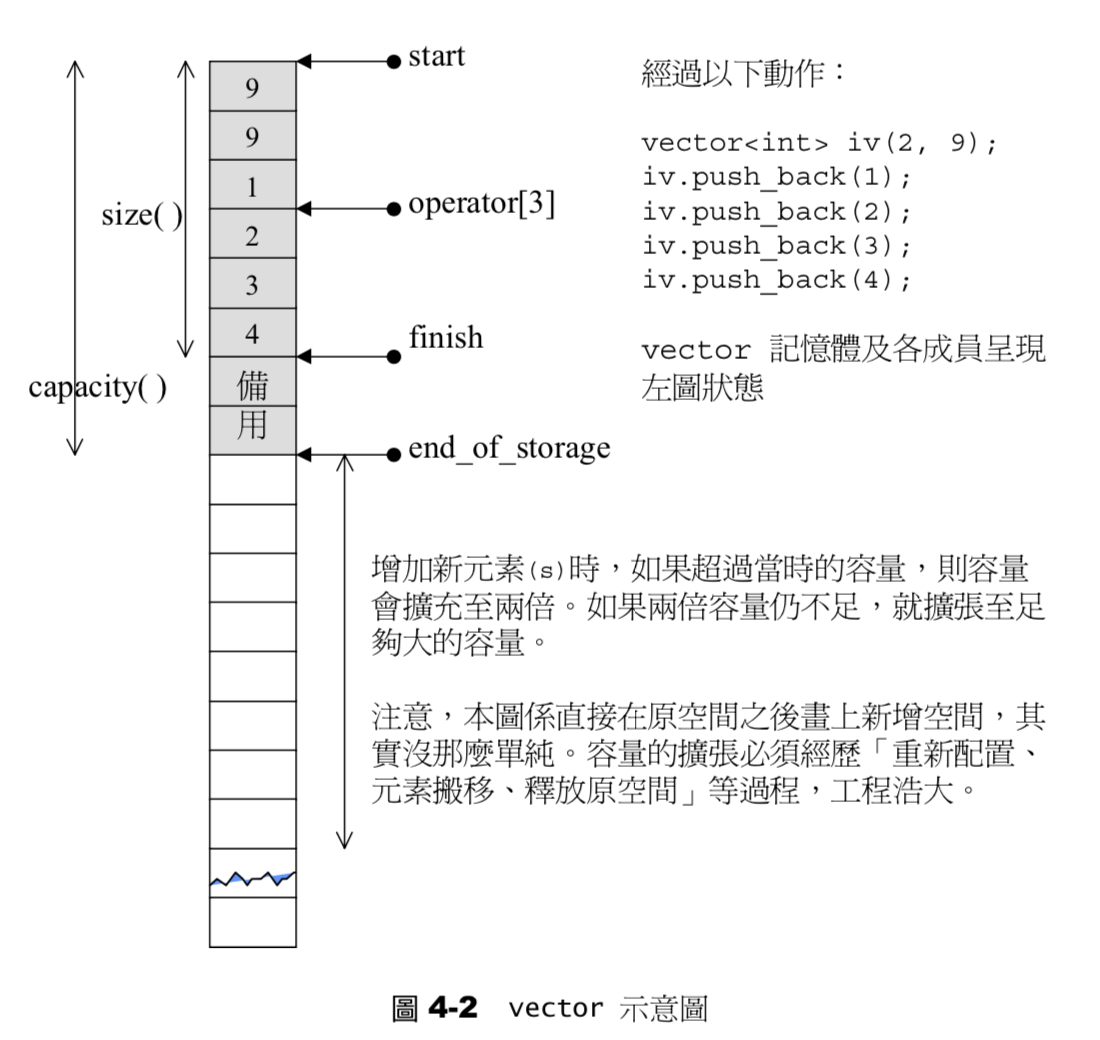
list

• 使用双向循环链表的结构进行数据存储，迭代器递增或者递减，需要通过链表的next和prev指针进行变更
• 与vector相比，不存空闲空间，任何位置的插入删除操作都是常数时间复杂度
• 获取链表长度的方式是通过遍历链表长度获取节点数量
• 通过一个空白的end节点实现正向与逆向遍历，如下图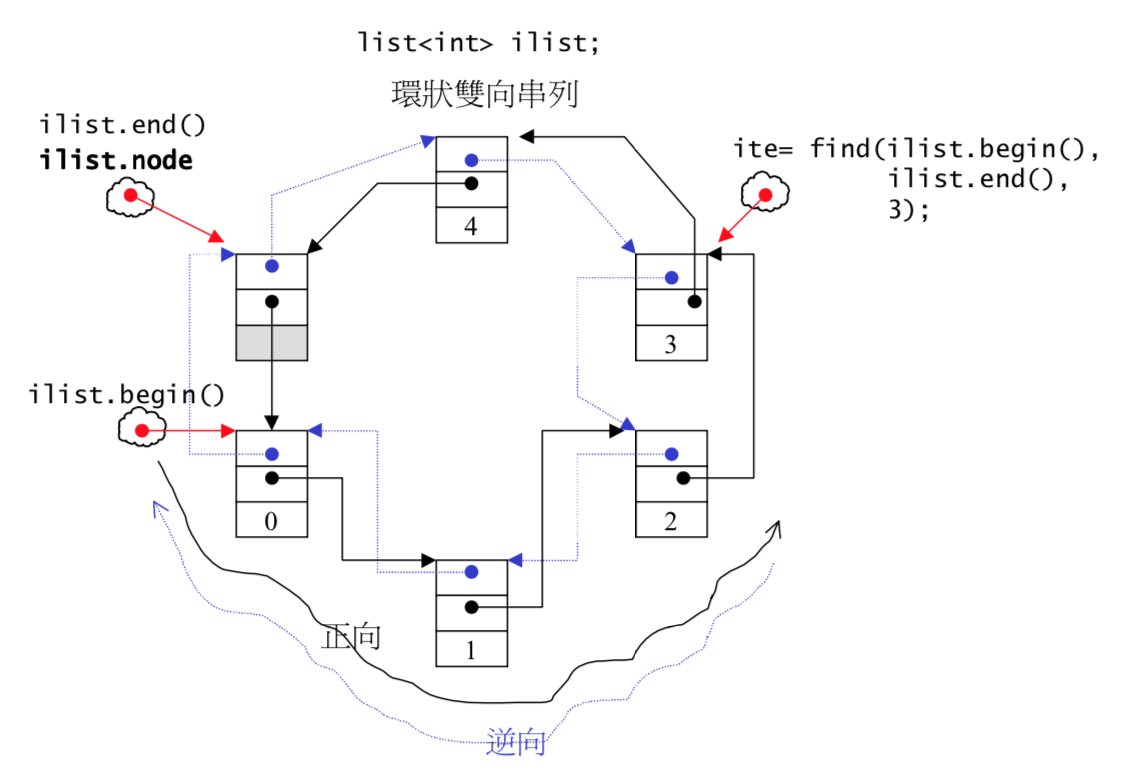
  

deque

• 使用复杂的两级存储设计，指针的遍历和移动的开销相比于vector要大很多，以至于对deque进行排序都不如将数据转到vector中，排好之后重新构造deque
• 设计示意如下图，通过数据结构map存储二级存储区域的起点，二级存储区域的大小是创建deque时声明好的。在start和end中都需要记录对应二级缓冲区的起始和结束位置以及当前头元素或者尾元素的下标和对应node结点的指针。其中map是一片连续存储空间，若大小不足时会进行调整（map两侧空闲空间差异较大时）或者扩容（两侧的空闲空间相差不大时）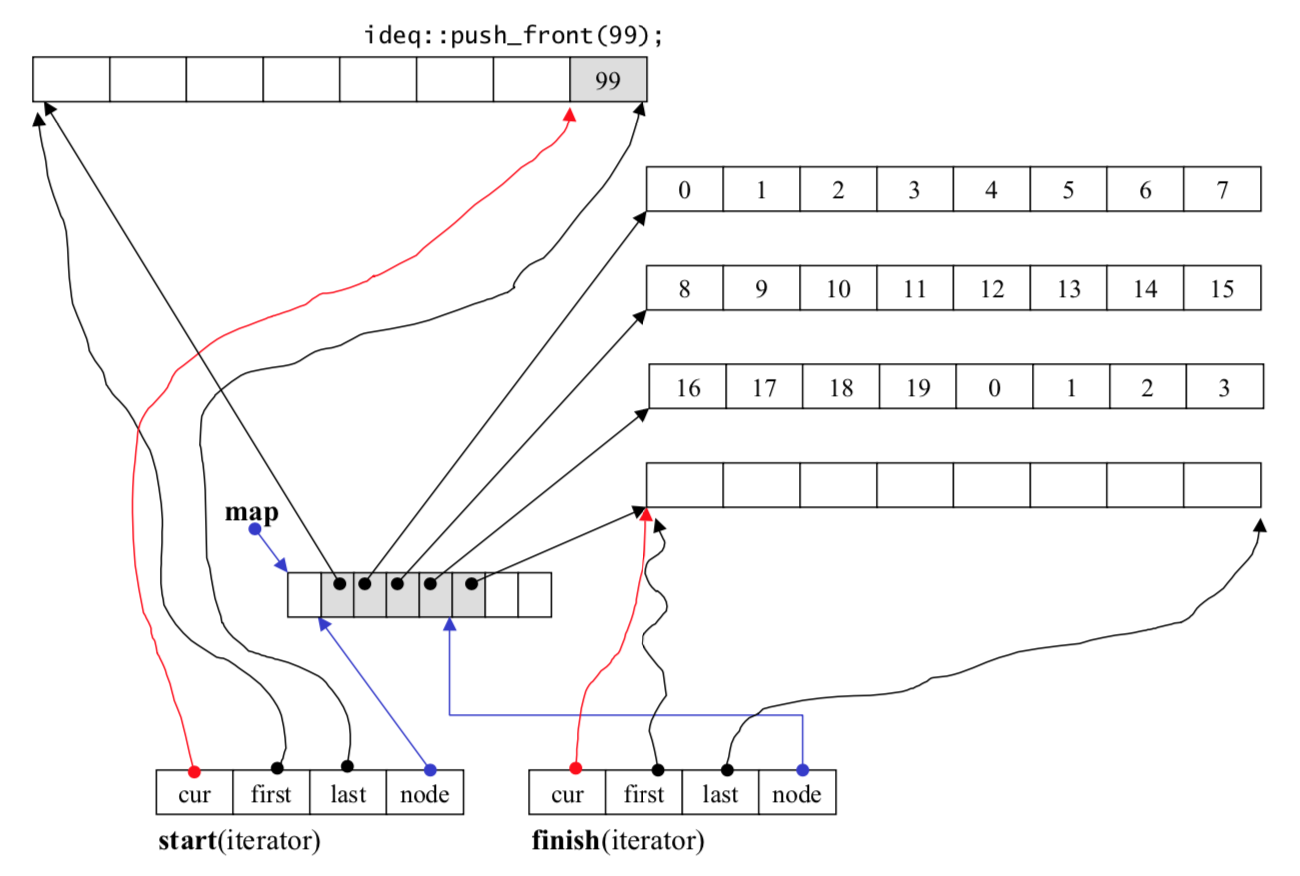
  

stack

• 缺省情况下使用deque（也可以选择使用list）作为底部结构，封装了接口
• 不提供迭代器

queue

• 缺省情况下使用deque（也可以选择使用list）作为底部结构，封装了接口
• 不提供迭代器

heap

• priority queue的幕后英雄，是一个implicit representation，我理解他是一个算法实现
• heap采用binary heap（complete binary tree）完全二叉树的数据结构
• heap算法依托于vector容器
• push_heap(RandomAccessIterator first, RandomAccessIterator last)代表底部容器的头尾（默认都是左闭右开），默认新元素已经放置到了最尾端。不断和父节点比较，直到将该元素放置到了正确的位置上。
• pop_heap(RandomAccessIterator first, RandomAccessIterator last)代表底部容器的头尾，会将尾元素和头元素交换位置，并从头向下放置
• sort_heap不断pop_heap向尾端放置当前范围内的最大元素
• make_heap从非叶子结点向前重排子数

priority queue

• 以vector为底部实现，利用heap进行处理

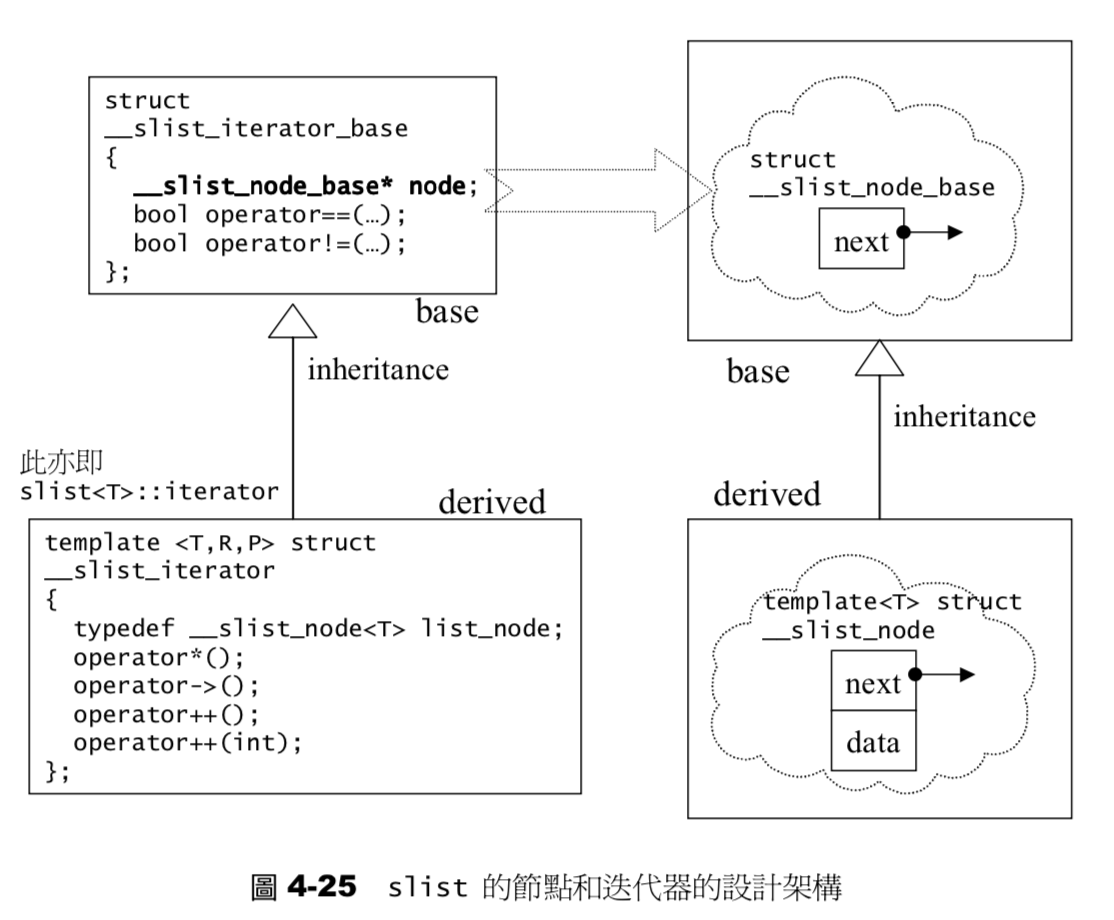
slist

• 单链表实现
• 运用了继承关系进行实现
  

Associative Container

tree

• AVL-tree
  • 导致不平衡的情况分为：左左、右右、左右、右左。
    • 其中的左左、右右都可以通过单旋转实现
    • 左右、右左通过双旋转实现
• RB-tree

  • RB 树规则

    • 节点非红即黑
    • 根节点是黑色的
    • 红色节点的孩子必须是黑色的
    • 任一节点到叶子节点的任一路径上的黑色节点数量必须相同

  • 插入规则，不满足下面规则就需要旋转&调整颜色

    • 新增节点为红色
    • 其父节点必须为黑色

  • 调整规则

    • 伯父为黑
      • 新增节点外侧插入、内侧插入（通过单旋转转变成外侧插入）
    • 伯父为红
      • 与伯父为黑相同的处理方式，但需注意曾祖父也为红色的时候，需要继续向上处理，会有麻烦
      • 针对上述情况，会有一个优化过程，将新增节点向上路径中，若X的两个孩子都为红色，就将X变成红色，两个孩子变成黑色。此时若与X的父节点颜色冲突，需要根据伯父为黑的规则旋转子树。

    情况	处理方式
    N和U都是红色	将P和U修改为黑色，G修改为红色
    N是P的左节点，同时U是黑色	对G进行一次右旋转，然后根据规则调整颜色
    N是P的右节点，同时U是黑色	首先对P进行一次左旋转，然后套用上一种调整情况

    基础添加

    

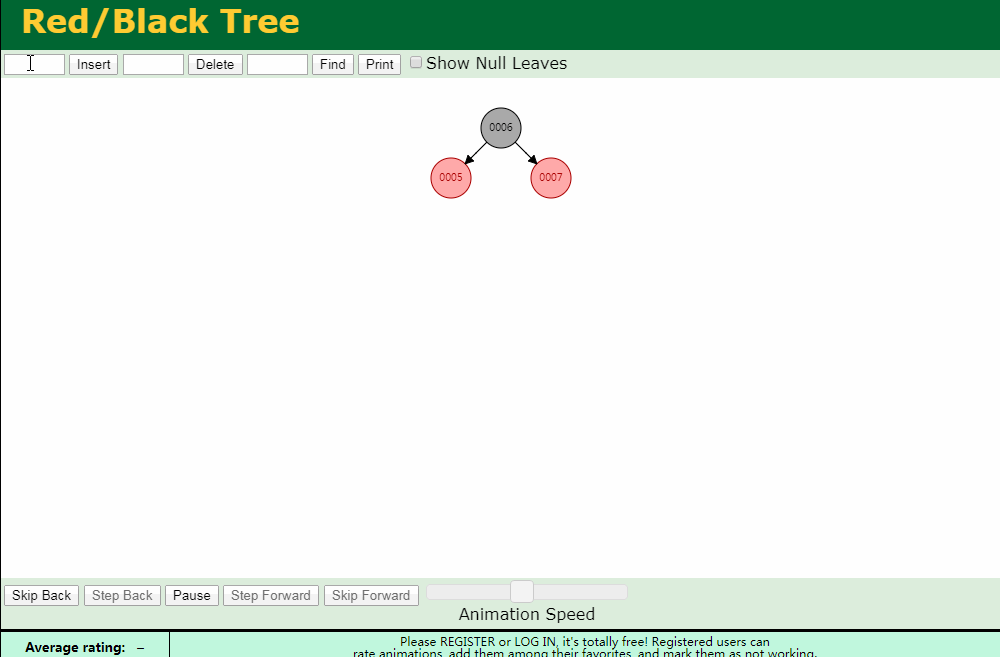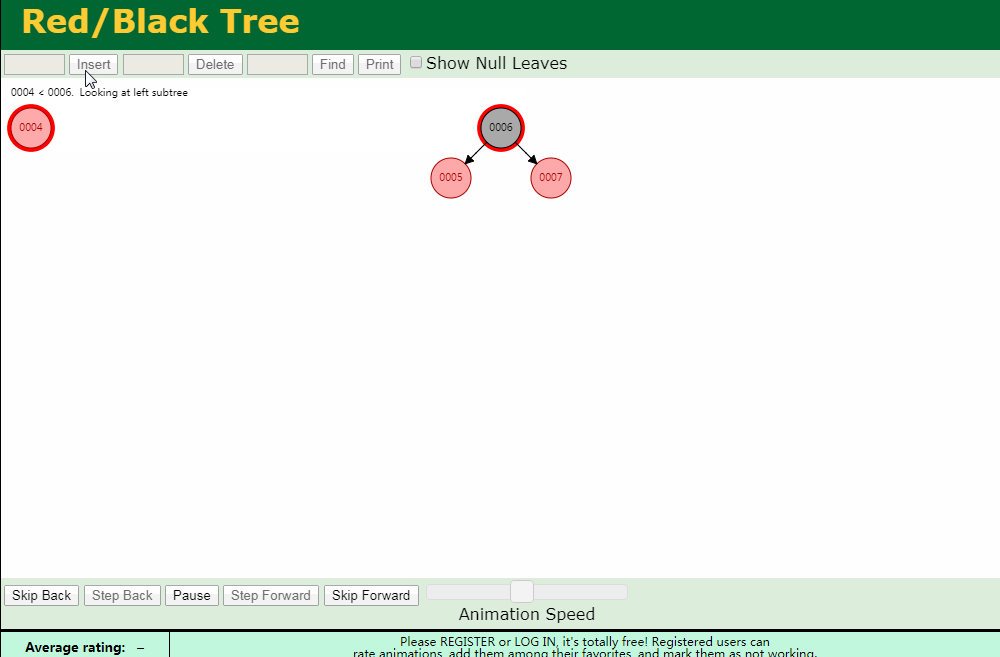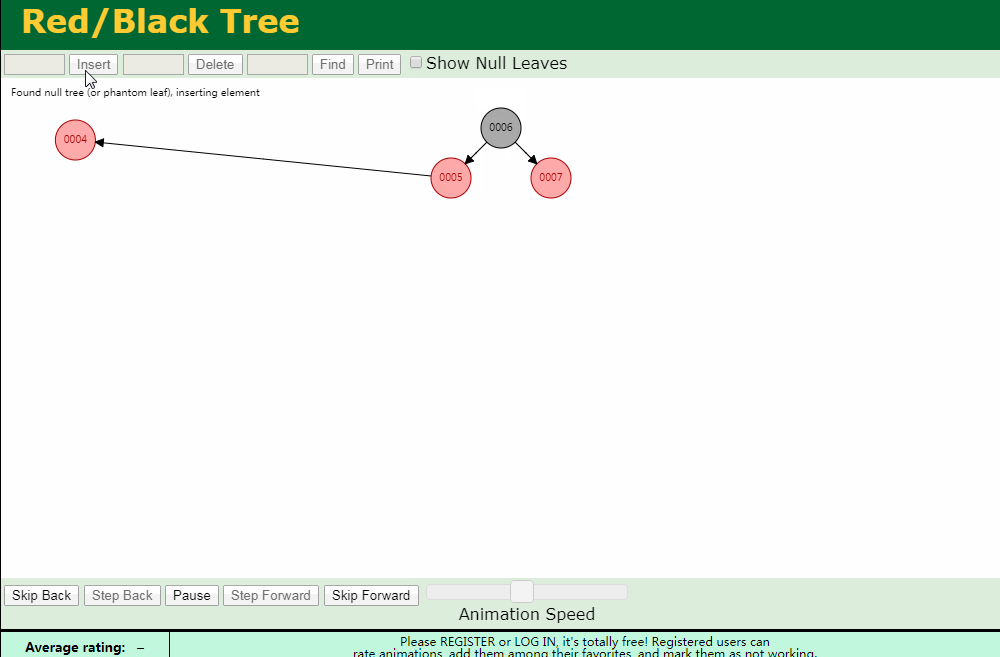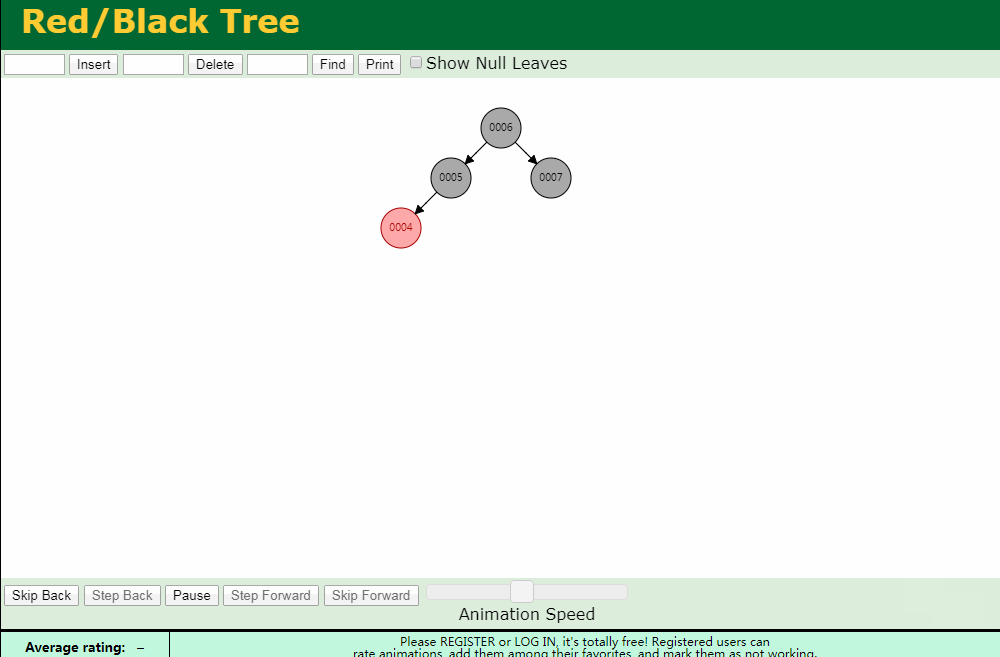
    左旋

    

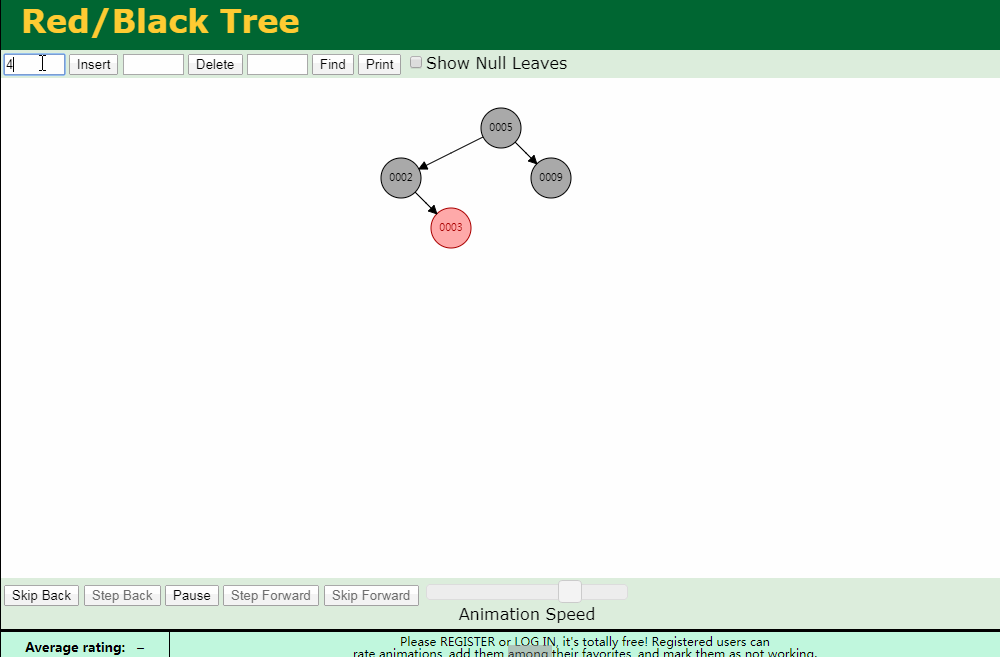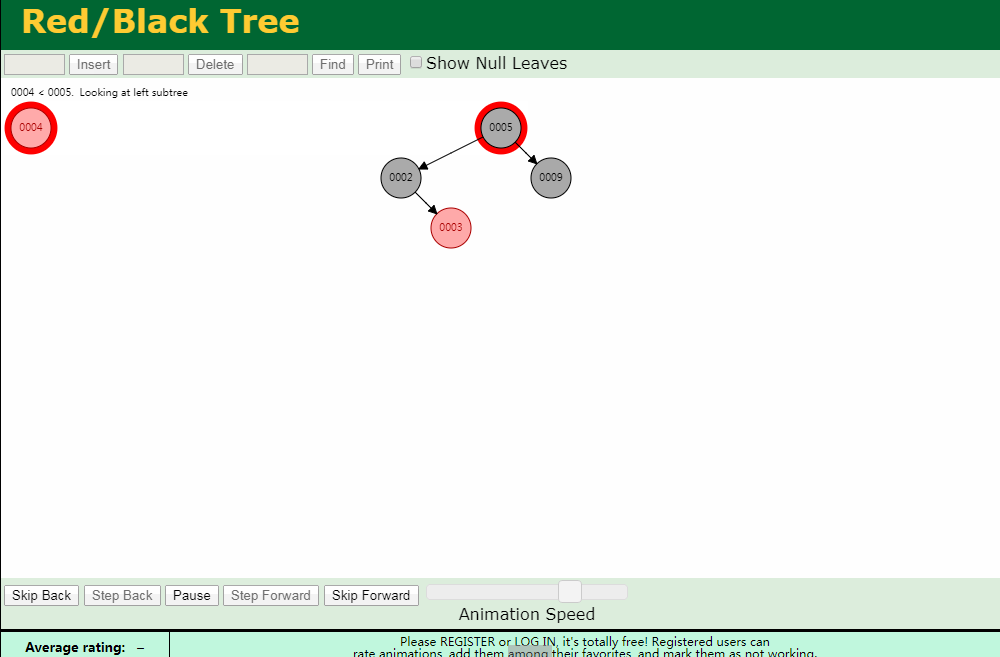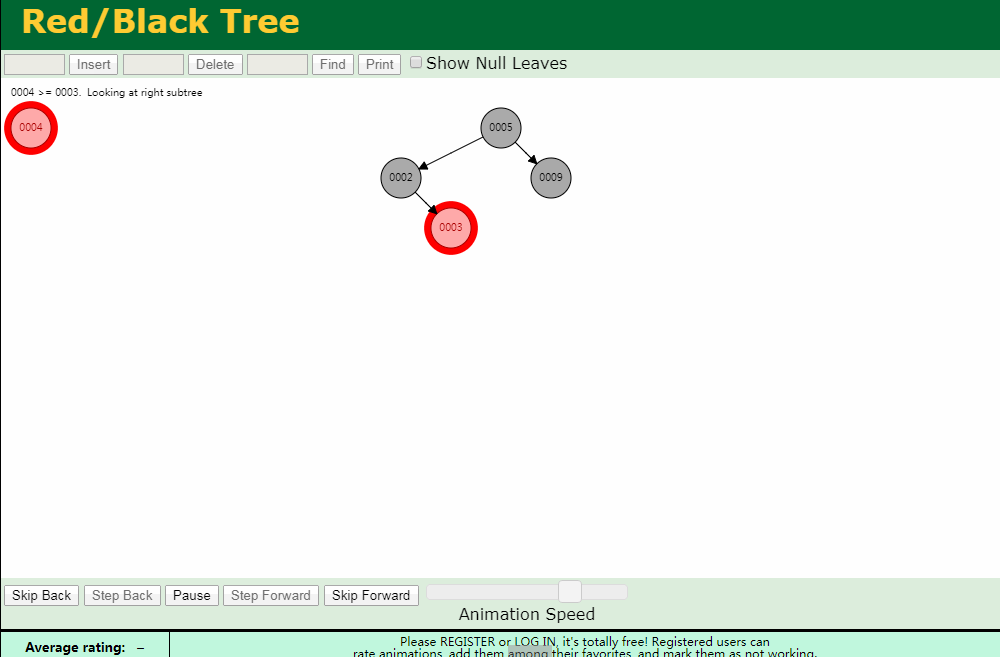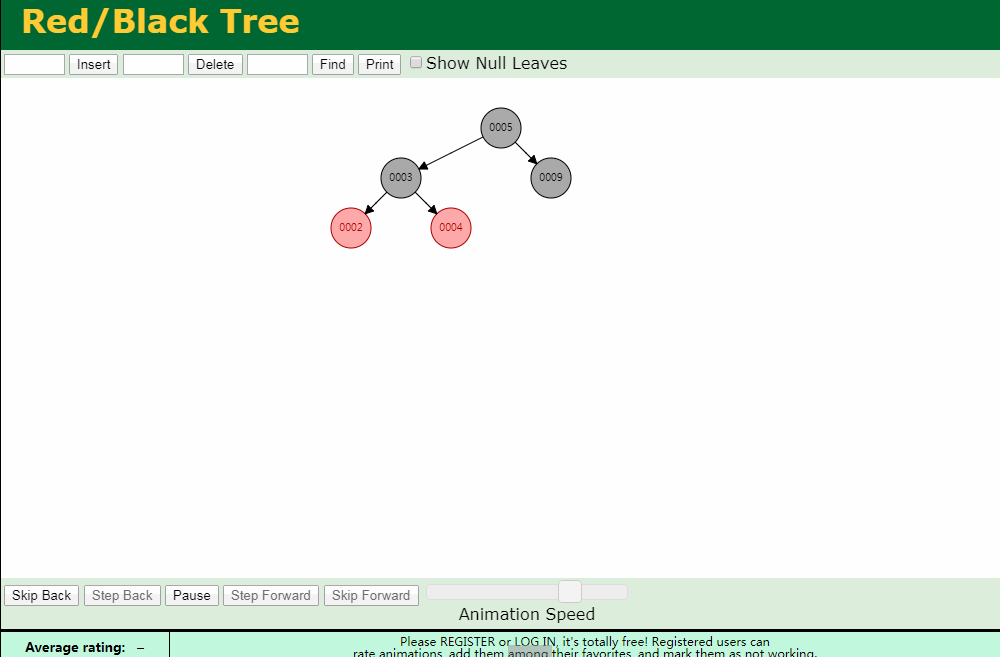
    右旋

    

set

• 基于RB-tree实现，迭代器被定义成constant，严禁修改
• 插入操作调用的RB-tree的insert-unique函数

map

• map中所有元素都是pair，key-value的形式

• 插入操作调用的RB-tree的insert-unique函数

• 有趣的设计，[]会先向RB-tree中插入一个带着默认值元素pair，若该pair已经存在，则返回已经存在的pair的迭代器；若该pair不存在，会被插入到树中，返回插入之后的迭代器。可能会造成tree的size变化

  typedef Key key_type; // 键值性别
  typedef pair<const Key, T> value_type; // 元素型别
  ...
  T& operator[](const key_type& k) {
    // 第一个first是插入之后元素的指针，第二个second是指针的实际内容 👇
    return (*(insert(value_type(k, T())).first)).second; 
  }

• upper_bound与lower_bound

  • upper_bound：上界

          iterator upper_bound (const key_type& k);
    const_iterator upper_bound (const key_type& k) const;

    Returns an iterator pointing to the first element in the container whose key is considered to go after *k*. 大于k的第一个元素

  • lower_bound 下界

          iterator lower_bound (const key_type& k);
    const_iterator lower_bound (const key_type& k) const;

    Returns an iterator pointing to the first element in the container whose key is not considered to go before *k* (i.e., either it is equivalent or goes after). 大于等于k的第一个元素

multiset

• 与set相比使用的是insert-equal函数

multimap

• 与map相比使用的是insert-equal函数

hashtable

• 不保证有序，采用哈希到桶，桶中拉链的方式。
• 针对hash之后的碰撞问题的解决思路有：线性探测、二次探测以及开链三种方法，STL使用的是开链的方式来解决碰撞问题
• hashtable大部分情况下的insert操作不会造成迭代器失效，但是当触发了rehash的时候，可能会造成迭代器失效，遍历不再完整的情况发生（小帕在帮忙debug算法题目的时候发现的问题，参考链接）

关于hashtable的具体细节

• hash function 举例：

  • 针对于char、int、long等整数型别返回的都是原值

  • 针对char数组的转换函数如下

    inline size_t __stl_hash_string(const char* s){
      unsigned long h = 0;
      for( ; *s; ++s){
        h = 5*h + *s; // 为啥呢？很多方法中的一种，为啥有效，懒得搞懂了
      }
      return size_t(h);
    }

• 负载系数：负载系数=元素个数/表格大小

• 桶的实现：vector<node*, Alloc> buckets

• 表格大小：也指桶的数量，虽然采用拉链算法不强制要求表格大小必须为质数，但是SGI仍以质数来设计表格大小。并事先准备了呈现了大约2倍增长的质数列表。会从表格中选取大于等于用户给定预期元素大小的最小的质数

  质数列表如下：53、97、193、...、4294967291ul

  为什么桶的数量需要是质数呢？

  省略掉数学推导，总结一句话就是：

  使用质数作为桶数，保证了我们即使是很简单的哈希函数，也可以保证整个hashteble的效率不会太低

• 判断是否需要resize的标准：元素数量如果大于桶的数量，就开始扩容，扩容之后的大小依旧是按照初始化表格大小的方式来计算（在质数列表中大于等于当前元素总数量的最小质数）

• resize的具体方法：

  • 根据resize的判断标准，构建新大小的桶

  • 逐桶每桶逐元素遍历，计算在新桶的位置

    __STL_TRY{
     for(size_type bucket = 0; bucket < old_n; ++bucket){ // old_n：旧桶的大小
        node* first = buckets[bucket]; // buckets：旧桶
        while(first){
          size_type new_bucket = bkt_num(first->val, n); // n：新桶的大小， bkt_num计算位于桶的位置
          // bkt_num会调用hash function得到一个可以执行模运算的数值，然后对n取模，n不传入的时候，默认使用bucktes的大小
          buckets[bucket] = first->next;
          first->next = tmp[new_bucket];
          tmp[new_bucket] = first; // tmp：新桶
          first=buckets[bucket];
        }
      }
      buckets.swap(tmp); // 交换存储的空间，交换之后的原迭代器仍有效
      // 释放tmp的空间 
    }

• 唯一插入

  • 插入的时候检查是否存在重复，如存在就返回已经存在的迭代器和插入失败的提示
  • 不存在的时候，会将新元素插入桶的头部，（新插入的元素，之后更有可能被访问到）

• 可重复插入

  • 存在重复的时候，插入到已经存在对象的后面
  • 不存在的时候插入桶的头部

• 整体清除，clear

  删除桶的每个节点，但是保留桶

  for(size_type i = 0; i < buckets.size(); ++i){
    node* cur=buckets[i];
    while(cur != 0){
      node* next = cur->next;
      delete_node(cur);
      cur=next;
    }
    buckets[i]=0; // 防止野指针的产生
  }
  num_elements = 0; // 声明节点数量为0

• 整体拷贝，copy

  void hashtable<...>::copy_from(const hashtable& ht){
    // 清空自己的buckets
    buckets.clear(); // 调用vector，清空所有的元素
    // 调整buckets的大小，若自己的空间不足，扩充至ht的大小，否则不动
    buckets.reserve(ht.buckets.size()); // 要求数组的容量大于等于size
    // 之前已经clear过了，所以buckets.end()就是数组的第一个位置
    buckets.insert(buckets.end(), ht.buckets.size(), (node*) 0); 
    __STL_TRY{
      for(size_type i = 0; i < ht.buckets.size(); ++i){
        if(const node* cur = ht.buckets[i]){
          // 复制好第一个元素
          node* copy = new node(cur->val);
          buckets[i] = copy;
          for(node* next = cur->next; next; cur=next, next=cur->next){
            copy->next = new node(next->val);
            copy = copy->next;
          }
        }
      }
      num_elements = ht.num_elements;
    }
    __STL_UNWIND(clear());
  }

基于hashtable实现的hashset、hashmap、hashmultiset以及hashmultimap不详细展开

Algorithm

sort

• vector

  • 数据量大时，采用快排，分段递归排序

    • 关于支点元素的选择，一般会在整段最左、中间和最右采样三个元素，然后取中值作为支点

      RandomAccessIterator __unguarded_partition(RandomAccessIterator first, RandomAccessIterator last, T pivot){ // 注意左闭右开
        while(true){
          while(*first<pivot) ++first; // 第一个比支点大于等于的
          --last;
          while(pivot<*last) --last; // 最后一个比支点小于等于的
          if(!(first<last)) return first;
          iter_swap(first, last); // 交换值
          ++first;
        }
      }

    • 当递归的次数过多时，通常会将排序方法修改成堆排，控制分割恶化

  • 数据量小时，采用插入排序（数据量大还是小一般被定义为5-20，具体根据机器来设定）

    • 会先检查边界，若要插入的元素比最左元素还小，直接整段向后复制
    • 将元素和前面的元素比较交换位置，有点类似于冒泡

• list

  • STL中的list采用了归并排序，而非快排

vector中采用快排的原因是，归并排序需要额外空间（使用额外的空间还意味着对象的拷贝，某些场景可能是致命的），这基本上是不太能接受的

list因为通过指针相互连接，使用归并也不需要额外的空间，除此之外，如果快排的话，链表不能使用一些优化方法，相比之下，还是归并比较合适

归并和快排对比表：

Functor

函数对象（又称为仿函数），可以作为参数传入的函数，例如自定义的大小比较函数。

自动配接

• unary_function，一元仿函数

  template<class Arg, class Result>
  struct unary_function {
    typedef Arg argument_type;
    typedef Result result_type;
  }
  
  // 实现一个仿函数，求负值
  template <class T>
  struct negate : public unary_function<T, T> {
    T operator()(const T& x) const { return -x; }
  }

• binary_function，二元仿函数

  template <class Arg1, class Arg2, class Result>
  struct binary_function {
    typedef Arg1 first_argument_type;
    typedef Arg2 second_result_type;
    typedef Result result_result_type;
  }
  
  // 实现一个二元仿函数
  template <class T>
  struct plus : public binary_function<T, T, T> {
    T operator() (const T& x, const T&y) const { return x + y; }
  }
  
  // less
  template <class T>
  struct less : public binary_function<T, T, bool> {
    bool operator() (const T& x, const T&y) const { return x < y; }
  }
  
  // 使用
  cout<<less<int>()(2, 3)<<endl;
  vector<int> iv;
  sort(iv.begin(), iv.end(), less<int>());

仿函数种类

• 算术类仿函数：加减乘除、模取、否定
• 关系运算类：等于、不等于、大于、大于等于、小于、小于等于
• 逻辑运算类：与、或、非
• 证同（返回自己）、选择（选择其中一个）、投射（只传回其中一个参数）

Adapter

对container、iterator和functor

contaier adapter

例如 stack 和 queue

iterator adapter

• Insert Iterator

  vector<int> arr{1,2,3,4,5,6};
  deque<int> id;
  copy(ia+0, ia+3, back_inserter(id)); // 通过迭代器插入

• Reverse Iterator

  将++变成向后操作，例如

  sort(iv.rbegin(), iv.rend()); // 6,5,4,3,2,1

• IOStream Iterator

  ostream_iterator<int> outite(cout, " || ");
  copy(iv.begin(), iv.end(), outite); // 输出：1 || 2 || 3 || 4 || 5 || 6 || % 

functor adapters

• 配接操作包括bind（系结）、negate（否定）、compose（组合）；

  • 不小于12的判断式

    not1(bind2nd(less<int>(), 12))

  • 实现\(f(g(elem))\)，其中\(f(x)=x*2\)，\(g(x)=y+3\)，可以描述为

    // 继承一元仿函数
    template <class Operation1, class Operation2>
    class unary_compose : public unary_function<typename Operation2::argument_type, typename Operation1::result_type> {
      protected:
        Operation1 op1;
        Operation2 op2;
      public:
        unary_compose(const Operation1& x, const Operation2& y):op1(x), op2(y) {};
        typename Operation1::result_type operator()(const typename Operation2::argument_type& x) const {
          return op1(op2(x)); // 函数合成
        }
    };
    // 为简化使用
    template <class Operation1, class Operation2>
    // 书中iterator获取参数类型的方法
    inline unary_compose<Operation1, Operation2> compose(const Operation1& op1, const Operation2& op2) {
      return unary_compose<Operation1, Operation2>(op1, op2);
    }
    
    int main(){
      int oa[] = {1,2,3,4,5};
      vector<int> a(oa, oa+5);
      ostream_iterator<int> outite(cout, " || "); // iterator adapter，将值输出到cout
      copy(a.begin(), a.end(), outite); cout<<endl;
      for_each(a.begin(), a.end(), compose(bind2nd(multiplies<int>(), 2), bind2nd(plus<int>(), 3))); // factor adapter
      copy(a.begin(), a.end(), outite); cout<<endl; // 因为for_each不改变元素原来的值，所以无效
      // 使用transform，将结果输出到另一个地方
      transform(a.begin(), a.end(), outite, compose(bind2nd(multiplies<int>(), 2), bind2nd(plus<int>(), 3))); cout<<endl;
      vector<int> b(a.size());
      transform(a.begin(), a.end(), b.begin(), compose(bind2nd(multiplies<int>(), 2), bind2nd(plus<int>(), 3)));
      copy(b.begin(), b.end(), outite); cout<<endl;
      return 0;
    }